TensorFlowの手書き数字認識チュートリアルからざっくりディープラーニングを勉強してみました

手書き数字画像の認識を行うTensorFlowのチュートリアルであるMNIST For ML Beginners[日本語訳]およびDeep MNIST for Experts[日本語訳]を通してディープラーニングについて勉強したので理解した内容をまとめてみました。的な話です。

TensorFlowとディープラーニングの概要

TensorFlow

TensorFlowとはGoogleが公開しているディープラーニングに対応した機械学習のライブラリです。Tensor(多次元配列/行列)のFlow(計算処理)をグラフ構造で定義し、それを元に演算を行います。演算処理が抽象化されているので演算デバイス変更などの対応が比較的容易と思われます。

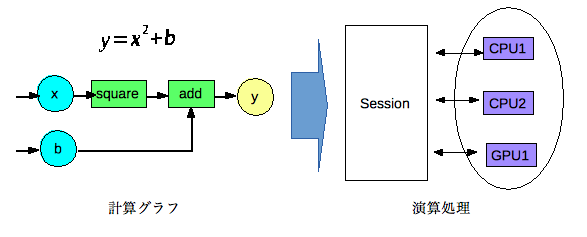
実装イメージ

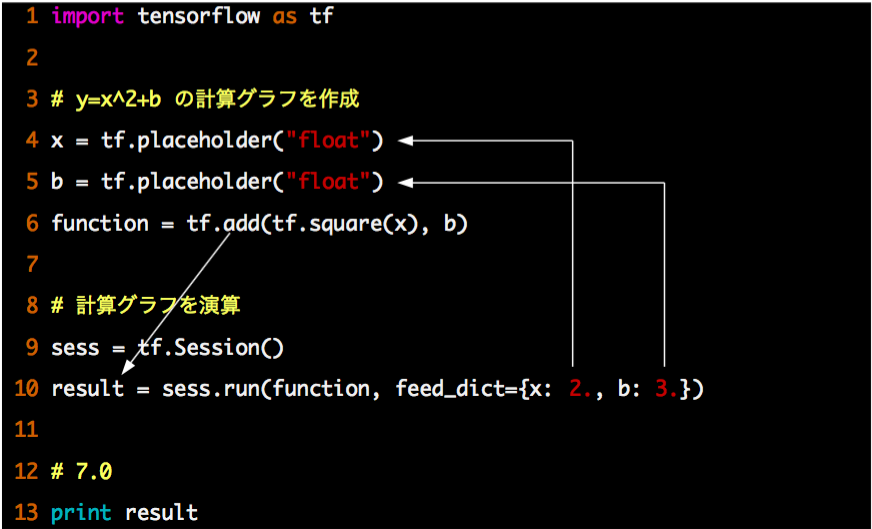
TensorFlowでy=x²+bにx=2,b=3を指定し計算する例です。変数はplaceholderとして定義しSessionに演算を指示するタイミングでfeed_dictで実際の値を指定します。

ディープラーニング

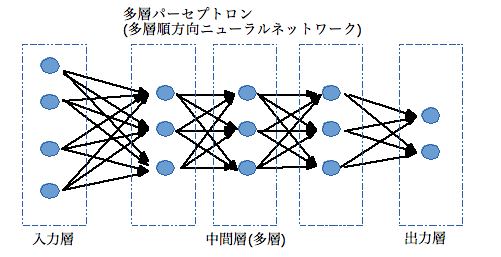
ディープラーニングとは、中間層を多層化して深く(Deep)したニューラルネットワークの機械学習(Learning)の事です。中間層が多いほど認識の精度が上がりますが学習が困難になります。学習の手法が考案され、ベンチマークテストで高い性能を示した事から注目されるようになりました。

チュートリアル1：MNIST For ML Beginners

まずはMNIST For ML Beginners[日本語訳]です。強引にまとめるとやりたいのことは次な感じと思います。

なんのこっちゃ？？という感じです。

前提知識のキャッチアップ

なので、まずは前提知識のキャッチアップです。(ざっくりイメージだけでも)

単純パーセプトロン

単純パーセプトロンとは、入力層と出力層だけの順伝播型ニューラルネットワークの事です。中間層が無い(深く無い)ネットワークですので、このチュートリアルはディープラーニングではありません。(ディープラーニングは次のチュートリアルにお預けです。)

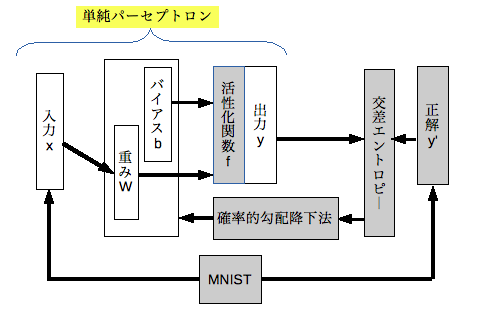
単純パーセプトロンの出力層の値(y)は、結合している入力層の値(x)と重み(W)を掛けた値の総和にバイアス/閾値(b)を加算し活性化関数(f)を適用する事で求めます。

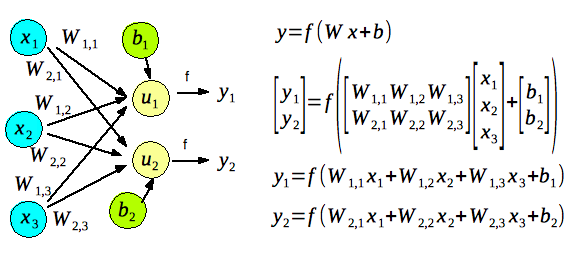
MNIST

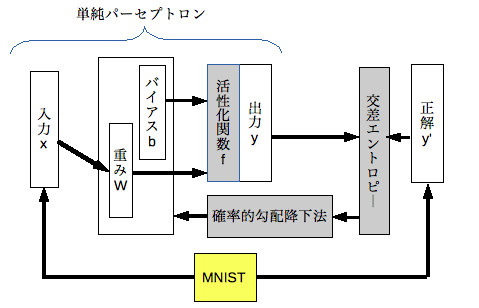
MNISTとは画像認識アルゴリズムのベンチマークに使われる手書き数字画像データセットです。このデータセットを認識できるように単純パーセプトロンを教師あり学習します。

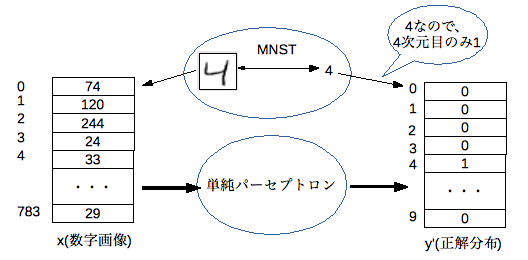
MNISTには画像と画像が表す数値の組が含まれます。各画像のサイズは28 x 28 ピクセルで各ピクセル値は 0 (白) ～ 255 (黒) です。60000枚の訓練データと10000枚のテストデータに分かれています。

今回は、入力層の値を「ベクトルに変換した画像(28 x 28 = 784次元)」に、出力層の値を「画像が表す数値次元目のみ1で他が0となる10次元ベクトル」として進めます。

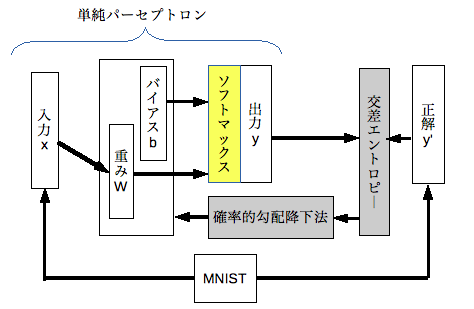
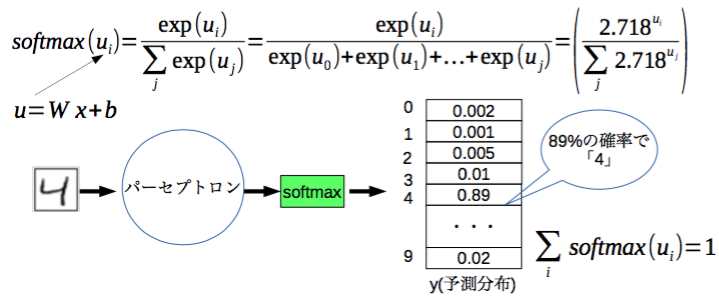
ソフトマックス関数

ソフトマックス関数とは「複数ある事象」のうち「ある事象」が起きる確率を求める関数です。多クラス分類問題の場合、出力層の結果を確率分布にしたいため活性化関数として用いられることが多いです。

ソフトマックス関数は、「ある事象」の場合の数をexp(場合の数)として計算するため、場合の数が大きい事象ほど確率を高く際立たせる事ができます。

各出力層の値は、出力層全体を事象全体としてソフトマックス関数で求める事により確率値となります。

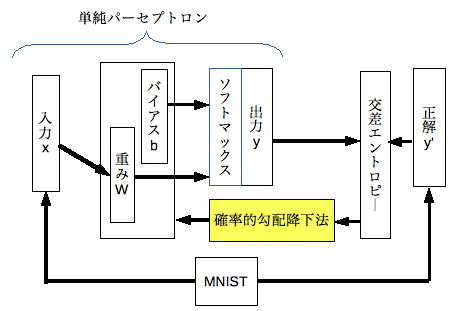
交差エントロピー

交差エントロピーとは、確率分布間のエントロピーの距離の事です。単純パーセプトロンが導いた結果と正解との差を求めるための損失関数として用います。損失関数は教師あり学習で用います。

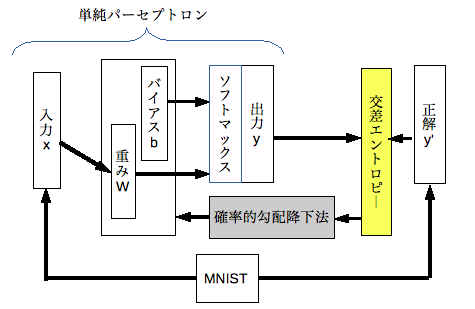
この関数は出力層で予測した確率分布と正解の分布が遠ければ差が大きくなります。

単純パーセプトロンの学習では、この損失関数の結果をペナルティとして小さくなるように重み/バイアスを調整します。

確率的勾配降下法

確率的勾配降下法とは、ある関数の極小値を算出する手法です。単純パーセプトロンの重みやバイアスを調整する教師あり学習のために用います。

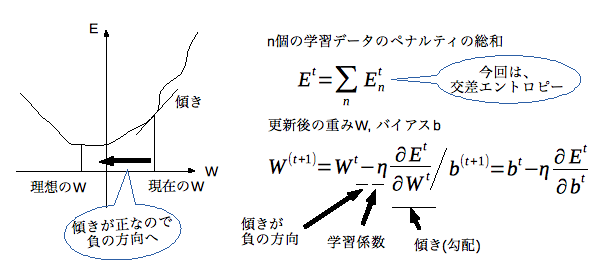
勾配降下法は、学習データに対するペナルティの総和(E)が小さくなる方向に重み(W)を更新し徐々に理想のWへと近づけていきます。動かす方向は傾き(ΔE/ΔW)が負となる方向になります。傾きに掛け合わせる学習係数(η)により動かす大きさが決まります。(バイアスも同様)

Eを全ての学習データを対象とせずに一部のデータに限定して計算量を抑えた方式が確率的勾配降下法です。

TensorFlowで動かしてみる

前提知識を(なんとなく)キャッチアップしたところでいよいよTensorFlowで動かしてみます！

計算グラフ

まず、単純パーセプトロンをTensorFlowで扱えるように計算グラフで表現します。ソフトマックス関数や交差エントロピー、確率的勾配降下法などの計算はTensorFlowが用意している関数で行う事ができます。

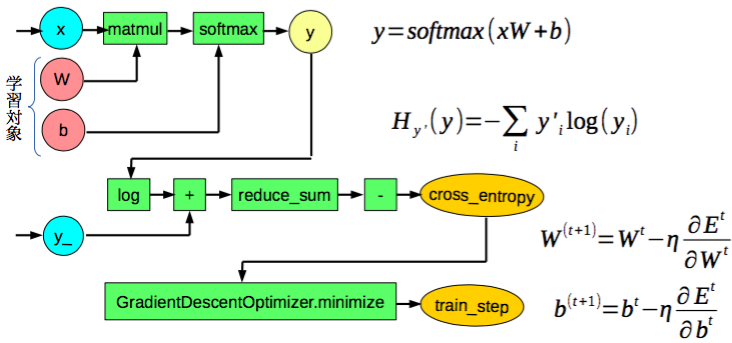
学習した結果を評価する部分です。

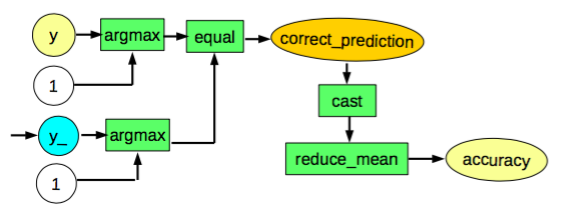
実装内容と実行結果

TensorFlowで数字画像の認識をします。まずはパーセプトロンの計算グラフを構築し初期化します。

次にMNISTデータセットを教師あり学習します。訓練データの100サンプルを1バッチとして1000バッチ分の学習を行います。

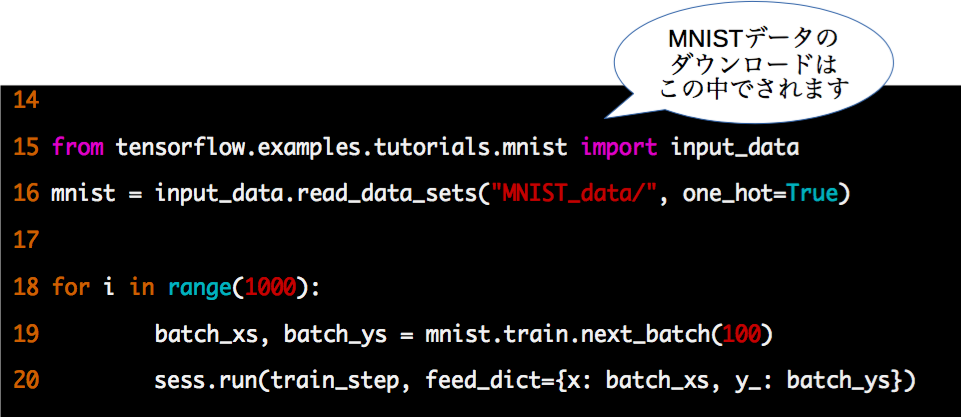
学習したモデルにテストデータを与えて結果を評価します。

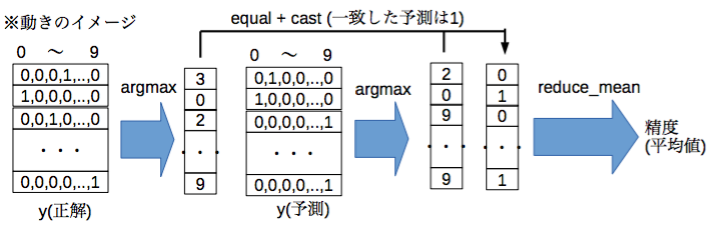
精度は約91％となりあまり良くないです。(今の最高水準は99.79%くらい？)

コードの全容

下記のとおりです。

import tensorflow as tf

x = tf.placeholder("float", [None, 784])
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
y = tf.nn.softmax(tf.matmul(x,W) + b)
y_ = tf.placeholder("float", [None,10])
cross_entropy = - tf.reduce_sum(y_ * tf.log(y))
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

print sess.run(accuracy,
           feed_dict={x: mnist.test.images, y_: mnist.test.labels})

チュートリアル2：Deep MNIST for Experts

次はDeep MNIST for Experts[日本語訳]です。強引にまとめるとやりたいのことは次な感じと思います。

良くワカリマセン。

前提知識のキャッチアップ

なので、まずは前提知識のキャッチアップです。(ざっくりイメージだけでも)

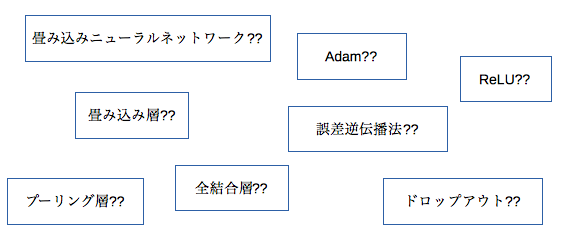
畳み込みニューラルネットワーク

畳込みニューラルネットワークとは、中間層として畳込み層とプーリング層を有する多層の順伝播型ニューラルネットワークの事です。画像認識の分野でよく用いられます。中間層を持った深いネットワークですのでようやくディープラーニングです。

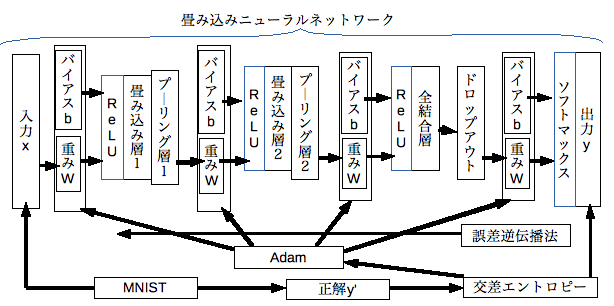
畳み込み層

畳み込み層とは、入力(x)に対して重みフィルタ(W)をスライドさせながら適用(畳み込み)した結果の集まりである特徴マップ(c)を抽出する層です。cはxの局所的な部分を抽象化した特徴量です。

結果に適用する活性化関数にはReLUを使います。

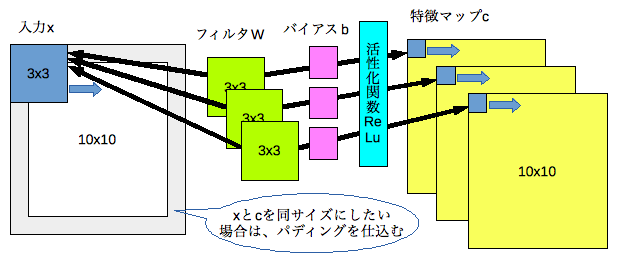
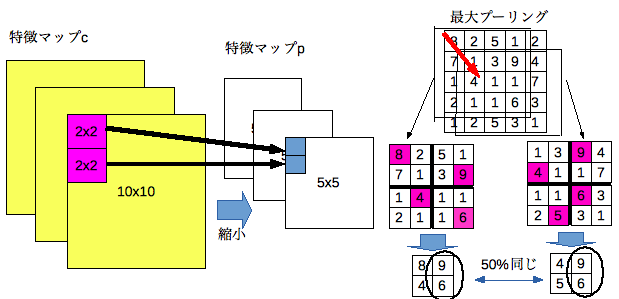
プーリング層

プーリング層とは、畳み込み層の結果である特徴マップ(c)を縮小する層です。局所的な部分の特徴を維持するような縮小を行うことにより位置変更に対する結果の変化を(若干ですが)抑えることができます。

最大値のみを取り出し縮小する「最大プーリング」などがあります。

全結合層

全結合層とは、隣接の層とユニットが全結合した層です。畳み込みニューラルネットワークでは畳み込み層やプーリング層の結果である２次元の特徴マップを１次元に展開します。

活性化関数にはReLUを使います。

Adam

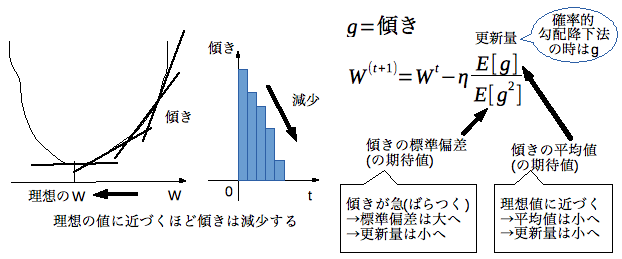
Adamとは、確率的勾配降下法の更新量を調整し学習の収束性能を高めた手法です。

確率的勾配降下法の(傾き)の部分を(傾きの平均値)/(傾きの標準偏差)とすることにより、始めの更新量は大きく学習が速く進み、理想の値に近づくほど更新量が減少し学習を収束させられる性質があります。

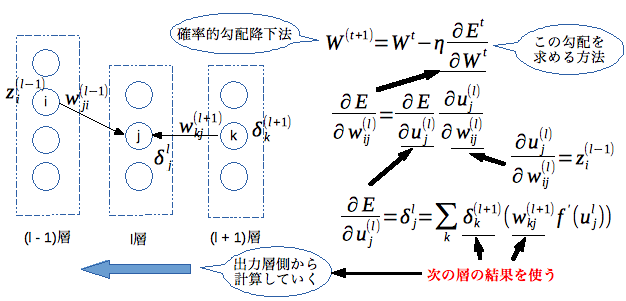
誤差逆伝播法

誤差逆伝播法とは、多層のニューラルネットワークにおいて各層の勾配を効率的に求める手法です。出力層から入力層に向かって誤差(ペナルティ)を逆伝播させながら求めていきます。

この勾配を用いて確率的勾配降下法やAdamによる重みの調整を行います。

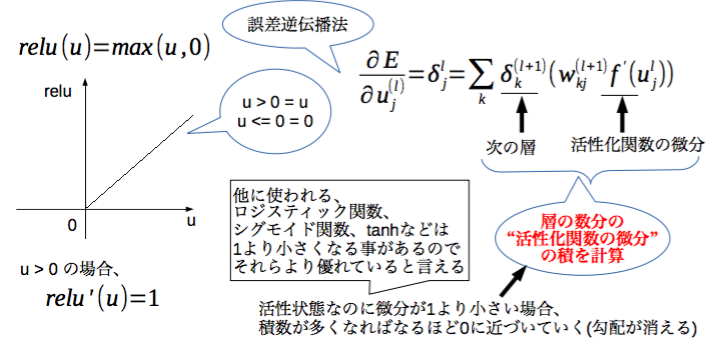
ReLU

ReLUとは、入力が0以下ならば0を出力し入力が0より大きいならば入力と同じ値を出力する非線形関数です。単純で計算量が小さく、微分すると活性状態なら1となるので誤差逆伝播法で活性状態の勾配が消えない性質がある事から活性化関数としてよく用いられます。

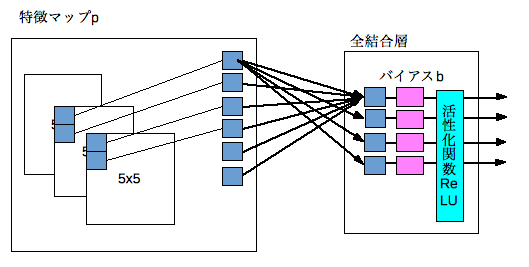
ドロップアウト

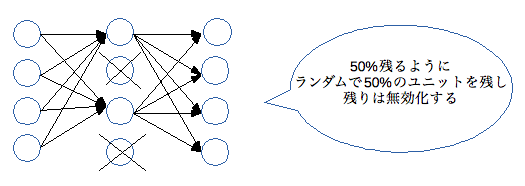
ドロップアウトとは、確率的勾配降下法等で多層ネットワークのユニットを確率的に選別して学習する手法です。ユニットの選別確率pを決めておき重み更新のたびに対象のユニットをランダムで選出します。

学習対象に過剰適合する過学習の状態を抑止する効果があります。

TensorFlowで動かしてみる

前提知識を(なんとなく)キャッチアップしたところでいよいよTensorFlowで動かしてみます！

計算グラフ

畳み込みニューラルネットワークを計算グラフで表現します。

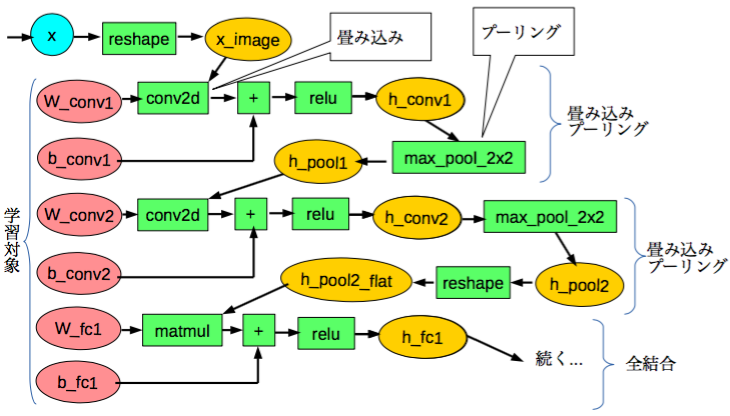
ReLUやドロップアウト、Adamや誤差逆伝播法などの計算はTensorFlowが用意している関数で行う事ができます。

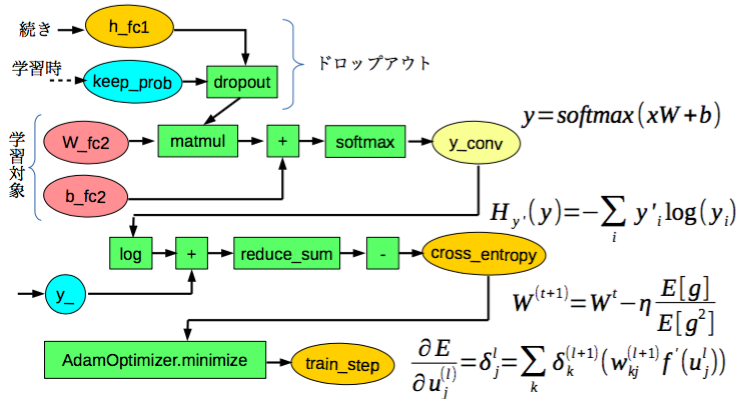
学習した結果を評価する部分です。(チュートリアル1と同じです)

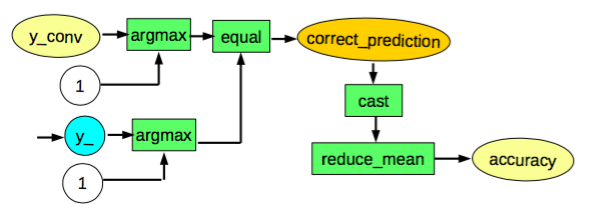
実装内容と実行結果

まず共通で使う処理を関数にしておきます。重みとバイアスの初期化、畳み込みとプーリングです。

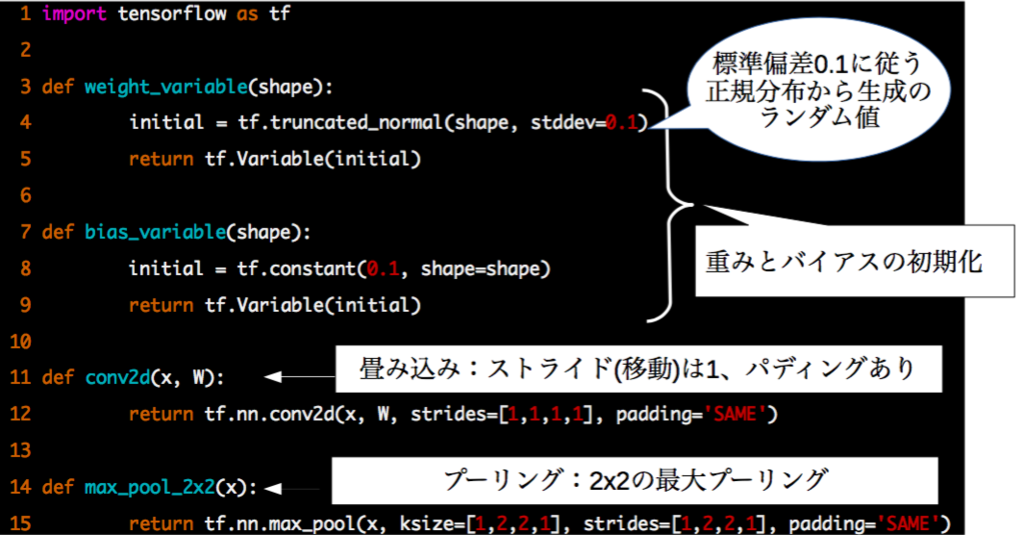
計算グラフを定義していきます。

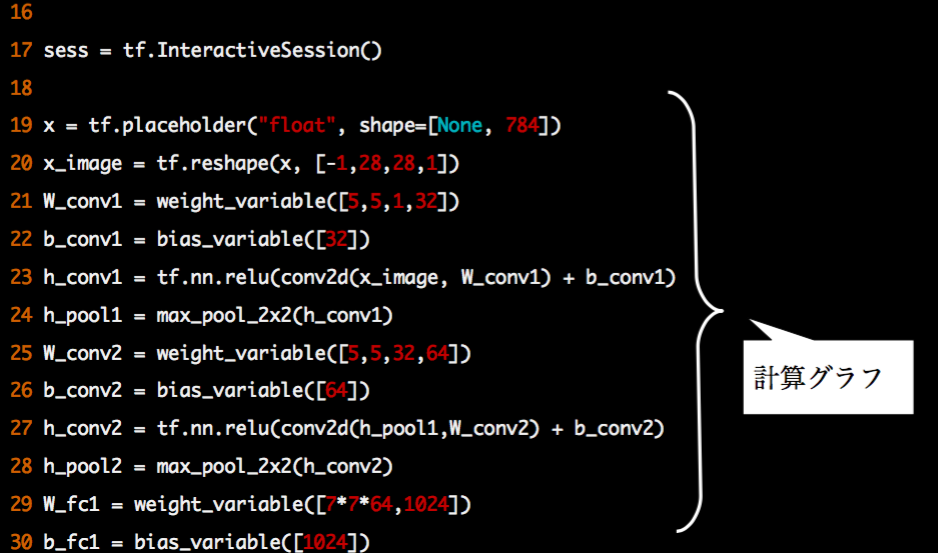
引き続き、計算グラフを定義していきます。

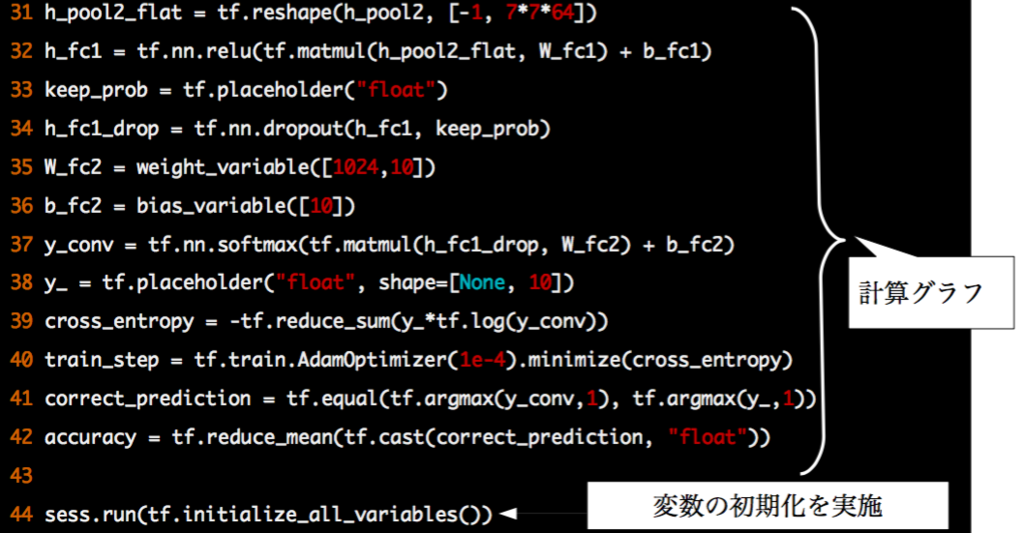
各変数のサイズの変化は下図のイメージです。

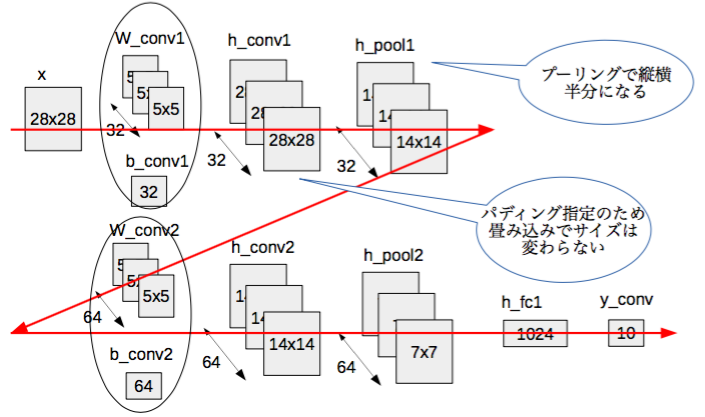
次にMNIST訓練データの50サンプルを1バッチとして20000バッチ分の学習を行います。ドロップアウト率は0.5にしています。

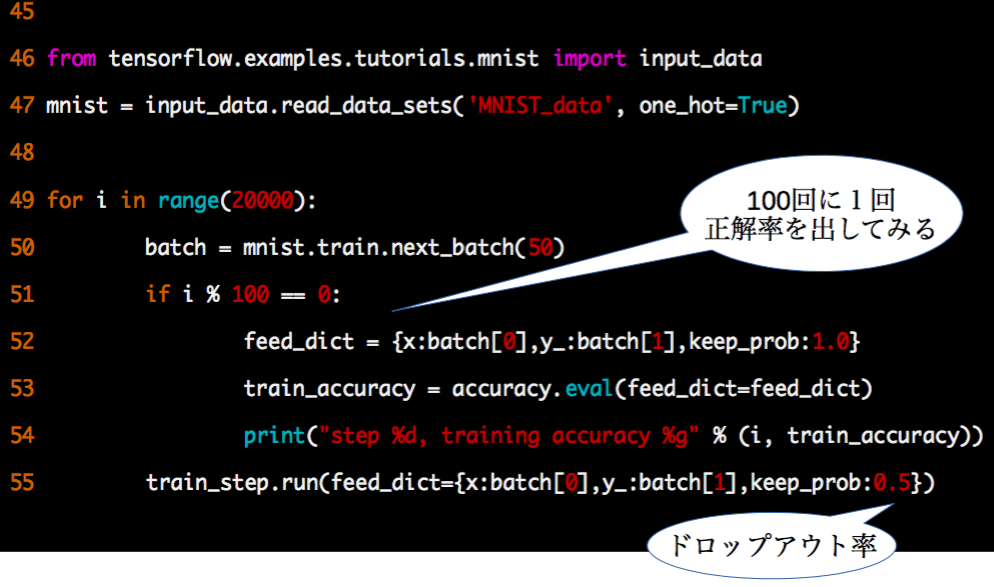
学習したモデルにテストデータで与えて結果を評価します。精度は約99.2％となりまずまずです。(今の最高水準の99.79%には及ばないけどチュートリアル1の約91%に比べたら)

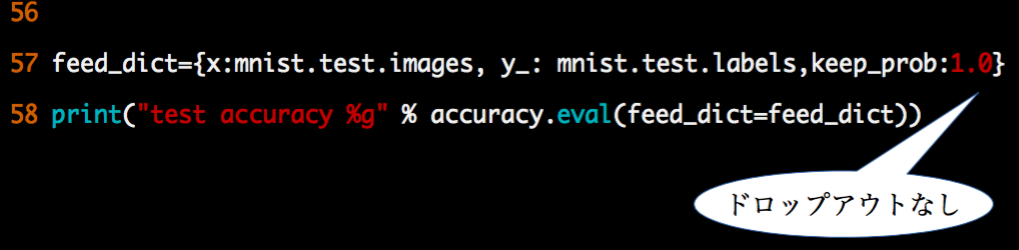
コードの全容

下記のとおりです。

import tensorflow as tf

def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)

def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)

def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1,1,1,1], padding='SAME')

def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')

sess = tf.InteractiveSession()

x = tf.placeholder("float", shape=[None, 784])
x_image = tf.reshape(x, [-1,28,28,1])
W_conv1 = weight_variable([5,5,1,32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
W_conv2 = weight_variable([5,5,32,64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1,W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
W_fc1 = weight_variable([7*7*64,1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
W_fc2 = weight_variable([1024,10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
y_ = tf.placeholder("float", shape=[None, 10])
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

sess.run(tf.initialize_all_variables())

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

for i in range(20000):
    batch = mnist.train.next_batch(50)
    if i % 100 == 0:
        feed_dict = {x:batch[0],y_:batch[1],keep_prob:1.0}
        train_accuracy = accuracy.eval(feed_dict=feed_dict)
        print("step %d, training accuracy %g" % (i, train_accuracy))
    train_step.run(feed_dict={x:batch[0],y_:batch[1],keep_prob:0.5})

feed_dict={x:mnist.test.images, y_: mnist.test.labels,keep_prob:1.0}
print("test accuracy %g" % accuracy.eval(feed_dict=feed_dict))

良く分からなかったところ

Deep MNIST for Experts[日本語訳]の重みの初期化の説明が良くわかりませんでした。なぜ微量のノイズで初期化するのか？対称性の破れとは何なのか？誰か詳しい人...

参考情報

次の情報を参考にさせていただきました。

情報源	メモ
TensorFlowを算数で理解する	y=x2+bの例
What is the class of this image ?	MNISTの最高水準の認識率
誤差逆伝播法のノート	勾配消失問題が分かりやすかったです
30分でわかるAdam	ざっくり理解できました
初めてのディープラーニング --オープンソース"Caffe"による演習付き	とっかかりに良かったです
深層学習 (機械学習プロフェッショナルシリーズ)	数式分かりやすかったです
イラストで学ぶ ディープラーニング (KS情報科学専門書)	深層学習 (機械学習プロフェッショナルシリーズ) で分からなくなった時に参照しました
深層学習 Deep Learning (監修:人工知能学会)	深層学習 (機械学習プロフェッショナルシリーズ) で分からなくなった時に参照しました

まとめ

TensorFlowのMNISTを認識するチュートリアルを通して単純なパーセプトロンと畳み込みニューラルネットワークの概要について調べてディープラーニングに対する理解を少しだけ深める事ができました。

とはいえ、まだまだ数式等の理解が足りないところも多く仕組みを完全に分かるところまでには達する事ができませんでした。もう少し学習が必要に思います。理解が誤っているところも多そうです。

今後は、画像認識だけでなく自然言語処理のためのディープラーニング技術などについても調査して何かに使ってみたいです。