2026-09-09

検証アジリティを追求するために index.html だけのスタンドアロン構成を試してみました

最近は個人開発で蔵書管理アプリを作っています。*1

「なぜ作るのか・どう検証するのか」というプロセスの話はnoteに書いてます。 note.com

今回はその技術・アーキテクチャ回をまとめてみます。*2

このアプリ、今はPSF（Problem-Solution Fit）検証フェーズです。
ドッグフーディングで検証サイクルを細かく高速に回しながら軌道修正を繰り返しています。それを たった1つの index.html で回しています。
この「ちゃんと作り込んでいない構成」が「いまのフェーズではむしろ正解だった」と思うので現在のスナップショットとして記録を残しておきます。

どんなアプリか
「index.html 1ファイル」で良かったこと
いまの実アーキテクチャ
作りながら下した判断
まとめ

どんなアプリか

まず「いまどんなアプリなのか」を機能で紹介します。前回のnoteから、UIも機能もだいぶ変わりました。

📷 バーコードでスキャン登録：
- ISBNを（スマホの）カメラで読み、多段の書誌API（openBD→NDL→Google Books）で書誌情報を自動補完
📚 蔵書一覧・検索：
- タイトル / 著者 / ジャンルで探す
🗄️ 置き場管理：
- 本棚をグリッド（本棚 × 行 × 列 × 手前/奥）で表現し、「どこにあるか」「奥に隠れた本」まで管理
🏷️ テーマで分類・検索：
- 本を「分類（グループ）」に登録（1冊を複数グループに入れてOK）。書誌から導く自動ジャンル（NDC）でも探せる
🔎 関連・同テーマ探索：
- 著者の名寄せ＋タイトル類似で関連本・同テーマ本を提示
🔄 棚卸し：
- 置き場ごとに最終棚卸し日を記録
💾 バックアップ：
- JSONで手動エクスポート / インポート
📱 ホーム画面設置（iOS）：
- apple-mobile-web-app メタでchrome-less（ブラウザUIなし）に起動。1枚でネイティブアプリぽいUX

「さがす」画面
スキャン所持チェック・置き場・分類（NDC／グループ）など、探し方が一望できます

蔵書一覧（詳細表示）
置き場（壁本棚6-6・奥）やジャンル・グループが一目でわかります

「index.html 1ファイル」で良かったこと

良かったことはシンプル。

1ファイルなので丸ごと共有しやすい
- （壁打ち相手にも、AIにもそのまま渡せる）
AIに実装してもらいやすい：
- 全体が1つのコンテキストに収まるので差分ではなく全体を把握して直せる
検証（壁打ち）→ 実装がシームレス：
- 構想・検証と同じ場所（今回はNotion）で、1ファイルなら丸ごとNotion AI（今回はOpus）に渡して実装まで一気通貫できる
外部依存が薄い（ビルドやフレームワークに依存しない）：
- 変更が速く、デプロイの摩擦がゼロ
アジリティが高い＝捨てやすい：
- 仮説が外れたら丸ごと捨てられる

AIは十分賢いので 「AIの実装を信じて、人間側の“可読性・テスト”を意図的に持たない」 割り切りをしていても検証は十分繰り返せている。

きちんと設計したりテストも書きたくなる気持ちはあるものの 「検証フェーズだから“いまは”凝らない」 感じ。
テストや構成をきちんとするのは下記が成立しなくなったら。それまでは今の構成で十分かなと。外部ユーザーに継続的に渡すとき、あるいは回帰が怖くて変更速度が落ちたら考える。

壊れてもデータはローカル（IndexedDB）＋JSONバックアップで戻せる
ユーザーが実質的に自分＋少数
外れたら丸ごと捨てる前提

あとNotion上でNotion AIと検証の壁打ちしてそのままコンテキストを引き継いで実装につなげられるのも1ファイルだからこそ。ただしこの体制も規模的に限界が近く、実装はそろそろClaude Codeなどローカルのツールへ移そうと考えている。

いまの実アーキテクチャ

以下はすべて、実物（hondana-v0.57.html / 全1,038行）から起こした構成です。*3
先に用語だけ揃えておきます。

置き場：
- 本の物理的な位置
- （本棚グリッド、押し入れ、段ボールなど）
自動ジャンル：
- 書誌の NDC → Cコードから導出する客観的な分類
書籍グループ：
- ユーザーが定義するテーマ分類
- 本に多対多で付く
- （1冊を複数に所属させてもOK）

全体構成

UI層 / スキャン層 / 書誌取得層 / 永続化層——これらがすべて1枚の index.html に乗っています。外部にあるのは書誌API群（openBD・NDL・Google Books・楽天）と、バーコード検出のpolyfill CDN、そして静的配信のVercelだけです。

スキャンの流れ

連続スキャンを止めないために、「登録は即座に完了（openBDのみ＝速い）／重い書誌取得（NDL・Google Books・楽天）は後追いのキューでenrich（情報付与）」という設計にしています。

スキャン中
上段のISBNバーコード（978…）を枠に、下段（192…）は価格JANでISBNじゃない

スキャン結果
「実は持ってる？」の所持チェックに加え、同じテーマの所持本まで一覧表示

「index.html だけ・DBも内部」の実装イメージ

骨格を抜粋します。CSSもJSも、そして DB（IndexedDB）も この1ファイルに同梱。DBすら外部サービスに置かず、ブラウザ内部に持ちます。*4

<!DOCTYPE html>
<html lang='ja'>
<head>
<meta charset='UTF-8' />
<meta name='viewport' content='width=device-width, initial-scale=1, viewport-fit=cover' />
<meta name='apple-mobile-web-app-capable' content='yes' />
<meta name='apple-mobile-web-app-status-bar-style' content='default' />
<meta name='theme-color' content='#f4f0e6' />
<title>本棚どこ？ — 蔵書位置メモ (v0.57)</title>
<style> /* 全画面ぶんのCSS（約340行）もこの1枚に同梱 */ </style>
</head>
<body>

<!-- ① 通常script：やっているのは iOS のキーボード/セーフエリアで崩れる高さの補正だけ -->
<script>
(function(){
  function upd(){
    var vv=window.visualViewport;
    if(vv && vv.scale && vv.scale>1.01){ return; }
    var h=vv&&vv.height?vv.height:window.innerHeight;
    /* … --app-h を更新して 100dvh のズレを吸収 … */
  }
  /* … resize / scroll で upd() を呼ぶ … */
})();
</script>

<!-- ② module：DBもスキャンも書誌取得もUIも、ぜんぶこの1本に集約 -->
<script type='module'>
const DB_NAME='hondana', DB_VER=4;
let db;
function openDB(){ return new Promise((res,rej)=>{ const r=indexedDB.open(DB_NAME,DB_VER);
  r.onupgradeneeded=(ev)=>{ const d=r.result;
    if(!d.objectStoreNames.contains('books'))   d.createObjectStore('books',{keyPath:'isbn'});
    if(!d.objectStoreNames.contains('shelves')) d.createObjectStore('shelves',{keyPath:'name'});
    if(!d.objectStoreNames.contains('cases'))   d.createObjectStore('cases',{keyPath:'name'});
    if(!d.objectStoreNames.contains('groups'))  d.createObjectStore('groups',{keyPath:'name'});
    /* … v3未満からの layer マイグレーション（「1. 置き場モデルの進化」で後述） … */
  };
  r.onsuccess=()=>res(r.result); r.onerror=()=>rej(r.error); }); }

// 書誌取得：openBD → NDL → Google Books →（楽天）の多段カスケード
async function fetchBook(isbn, opts){ /* … */ }

// バーコード検出：native優先、無ければ polyfill を動的import
async function getDetector(){
  if(!('BarcodeDetector' in window)){
    const mod=await import('https://esm.sh/@undecaf/barcode-detector-polyfill@0.9.20');
    window.BarcodeDetector=mod.BarcodeDetectorPolyfill;
  }
  return new window.BarcodeDetector({ formats:['ean_13'] });
}

// 起動：DBを開いて描画（全部このmodule内で完結）
(async ()=>{ db=await openDB(); await refreshLocSelectors(); await render(); })();
</script>
</body>
</html>

ビルドもフレームワークもありません。通常の <script> はiOSの表示調整（高さ補正）だけ。DB（IndexedDB）・スキャン・書誌取得・UI・起動処理まで、すべて1本の <script type="module"> に収まっています。

永続化＝IndexedDB

DB_NAME='hondana' / DB_VER=4。4つのストアで構成しています。

ストア	キー	役割	主なフィールド
books	isbn	蔵書	title, author, publisher, cover, shelf(置き場), groups, ndc, ccode, genre など
shelves	name	置き場	type, caseName, row, col, layer(front/back), labels, lastInventoriedAt
cases	name	本棚（グリッド）	rows, cols
groups	name	書籍グループ（多対多の実体）	name

データモデル：置き場軸とテーマ軸

置き場軸：
- books.shelf → shelves
- 棚のマスは本棚 × 行 × 列 × 手前/奥から名前を生成
- 「見えない蔵書」＝ layer==='back'、もしくは押し入れ・段ボール・平積み
テーマ軸：
- books.groups[]（多対多）
- 加えて自動ジャンル（NDC）でも探せる

分類でさがす（NDC）
「分類あり 1,229冊（97%）」
——書誌のNDC／Cコードから自動でジャンル付けした客観分類

依存の実体（正確に）

「外部依存なし」と言い切るのは不正確なので、正確に書いておきます。

ビルド / フレームワーク / npm ＝なし
- （<script> 2本、動的importはpolyfillのみ）
実行時の外部：
- openBD・NDLサーチ・Google Books・楽天Books（任意）・esm.sh（polyfill CDN）・Vercel（静的配信）

つまり正確には「ビルド依存ゼロ・実行時の外部はAPIとCDN polyfillのみ」です。

作りながら下した判断

アプリのドッグフーディング・検証サイクルにてこのアーキテクチャで実装する過程で、実際に行った具体的な軌道修正や判断を3つ紹介します。

1. 置き場モデルの進化と、DBマイグレーション

検証の話（過程 → 仮説 → 変更 → 検証結果）

過程：
- 最初はフラットな置き場リスト＋自由テキストの位置メモで始めた
- だが実物（壁本棚7段×7列＝49マス）に向き合うと、各マスの名称を自由テキストで表すことも特定することも自分には難しかった
- 家の収納は平面のリストじゃない、と気づく
仮説：
- 位置を「本棚 × 行 × 列」のグリッドで正式に表せば、実物の棚と一対一で対応でき、入力も検索も成立するはず
変更：
- フラットな棚
  - → 自由テキストの位置メモ（実サイズで破綻）
  - → 本棚 × 行 × 列のグリッド化（cases ストア追加・DB_VER=2）
- さらに「二重差し（同じマスの奥にも別の本がある）」をドッグフーディングで踏み、手前/奥のバッジ（layer(front/back)）を追加（DB_VER=2→3）。
- 「見えない蔵書」は layer==='back'、もしくは押し入れ・段ボール・平積みと定義した
検証結果：
- 仮説は正しかったと判断
- グリッド＋手前/奥のモデルは実物の棚と素直に一対一で対応し、登録も検索も成立した
- 同時に適用範囲の境界も見えた
  - ——手前も奥も背表紙が見えないクローゼットの積読タワーのような入れ物だけは、グリッド化せず「押し入れ」種別＝丸ごと見えない置き場として扱うのが正解で、手前/奥グリッドが効くのは「中身が見える棚」だけだと分かった

実装の話（必要になった変更 → 良かったこと → 割り切ったこと）

必要になった変更：
- 既存の shelves の行には layer が無い
  - → DBマイグレーションが必要に
- 正規化DBなら ALTER TABLE ＋移行スクリプト＋運用となるところを、IndexedDB の onupgradeneeded の中で数行当てて済ませた

// openDB() の onupgradeneeded 内（v3 未満からの移行）
if (ev.oldVersion < 3 && tx) {
  const st = tx.objectStore('shelves');
  st.openCursor().onsuccess = e => {
    const c = e.target.result; if (!c) return;
    const v = c.value;
    if (!v.layer) { v.layer = (v.type === '棚マス') ? 'front' : 'none'; c.update(v); }
    c.continue();
  };
}

良かったこと：
- index.html ＋ IndexedDB ＋“スキーマは緩い”割り切りだからこそ、モデルの進化を数行で回せた
- もし正規化DB＋スキーマ管理で作り込んでいたら、この layer 追加はスキーマ変更＋マイグレーション運用のコストが乗る変更だった
- データモデルを気軽に育てられること自体が、検証速度に効果的
  - ——モデルが固まりきる前のいまだからこそ、この緩さは正解
割り切ったこと：
- 棚マス以外は layer を一律 'none' に簡略化
- 参照整合性もDBの制約ではなくアプリ側（putBook / putLoc）で担保＝壊れる余地は残すが、単一ユーザー・ローカルなので許容した

壁本棚（7段×7列）のグリッド
各マスの冊数と「奥◯◯」＝見えない蔵書（layer==='back'）
本棚 × 行 × 列 × 手前/奥でマス名を生成します

2. 分類の主語を「置き場」から「本」へ

検証の話（過程 → 仮説 → 変更 → 検証結果）

過程 / 最初の仮説：
- 「本の置き場所にテーマのラベルを付ければ、それがそのまま分類になるのでは」
- 実装は shelves.labels[]（置き場所にラベルを持たせ、本の分類はそのマスから動的に導出する多対多）、「ラベルでさがす」UIも用意
最初の検証で気付いた誤りと新しい仮説：
- 自分で使い込む（ドッグフーディング）と、分類したい対象は"場所"ではなく"本"だった
  1. 本は複数のテーマにまたがる
  2. 同じテーマの本が複数の置き場に散る。
- 決定打は「1マスに複数テーマが同居する」問題だった
  - ——たとえばDB本とネットワーク本が同じマスにあると、そのマスには「DB」「ネットワーク」「技術書」をまとめて付けるしかなく、「DB」で引くとネットワーク本まで一緒にヒットする
  - 物理の1マスはテーマ混在が前提なので、"場所"を主語にする限りテーマ単位の絞り込みは原理的にできない
変更：
- 分類の主語を「場所」→「本」へ
- 1冊が複数テーマOKの多対多（books.groups[]）に
- 置き場側のラベルは、そのマスにある本の groups[] を集計した射影として自動導出に切り替え、手動のラベル編集は廃止
検証結果：
- 作り替えた「本を主語にした多対多」が実際に"探しやすさ"を生むか
  - ——この新しい仮説は、まだ使い込みで確かめられていない（価値検証はこれから）。

実装の話（必要になった変更 → 良かったこと → 割り切ったこと）

必要になった変更：
- 分類の実体を shelves.labels[] → books.groups[]（本に多対多で付く）へデータモデルごと作り替え
- ただし置き場側の表示は捨てず、「その置き場にある本の groups[] を集計したピル」＝書籍グループの射影として残した
- 旧 shelves.labels[]／「ラベルでさがす」UIは呼び出し元を外して非表示にし、データ構造だけが"化石"として残る
良かったこと：
- セクション1が"緩いスキーマだから安く直せた"話なら、こちらはモデルの主語ごと作り替えても、UI（見せ方）は射影で保てたという学び
- データの持ち方を変えつつ、ユーザーから見た置き場ビューは壊さずに移行できた
割り切ったこと：
- 旧 shelves.labels[] を消さずに残したのは意図的な技術的負債
- 呼び出し元を外して非表示にするだけに留め、「いつ消すか」は保留した（単一ユーザー・ローカルなので実害が小さい）。

分類（グループ）でさがす
「オライリー 75冊・4か所に散在」「技術書 3冊・3か所に散在」
——同じテーマの本が複数の置き場に散る様子が、そのまま可視化されています

3. 選ばなかった複雑さ

最後に、意図的に採用しなかった 選択肢と、その理由・“選択肢を採用する条件”を並べます。複雑さを“理解した上で選ばない” ことも重要。

Supabase（Postgres）の即導入：
- リレーショナル・認証・同期は魅力
- でもいまは単一ユーザー・ローカル完結で足りる
- スキーマ設計 / マイグレーション運用 / ネット必須が検証速度を殺す
  - → IndexedDB の緩いスキーマで“育てる”方を選んだ
- 選択肢を採用する条件
  - ＝外部ユーザーに継続的に渡すとき
フレームワーク（Next / React など）：
- コンポーネント化・型・エコシステムは魅力
- でもビルドの摩擦と「1ファイルで丸ごとAIに渡せる」性質を失う
- 素のDOM操作で回る規模
- 選択肢を採用する条件
  - ＝画面数・状態が1ファイルで破綻する規模
ビルド / 型 / テスト：
- 型安全と回帰テストは魅力
- でも「AIが全体を読んで直す→動かして確かめる」高速サイクルと引き換え
- 検証フェーズでは意図的に持たない
- 選択肢を採用する条件
  - ＝回帰が怖くて変更速度が落ちた瞬間
オフラインPWA化（Service Worker）：
- “できる”けれど、あえて やっていない
- むしろ検証中はキャッシュのstaleを嫌って、コードで Service Workerを明示的に解除し、キャッシュを削除 している
  - （＝毎回最新を取りに行く）
- iOSのホーム画面設置（apple-mobile-web-app）だけを使い、PWA化そのものは“理解した上で選ばない”
- 選択肢を採用する条件
  - ＝オフライン要求やアプリシェルの再訪コストが実利用で出たとき

いずれも「できない」のではなく、「いまのフェーズでは選ばない」。過剰に設計しないことの設計——いつ・何を・どのトリガーで入れるかだけを先に決めておく、というスタンス。

現状（PSF検証）は index.html ＋ IndexedDB ＋ Vercel静的配信。本格開発フェーズでは、永続化を Supabase(Postgres)、フロントを Next、必要に応じてちゃんとしたバックエンドも*5——とリアーキしていく想定です。開発体制も、いまは Notion AI で実装していますが、規模的に限界が近いので、実装は Claude Code などローカルのツールへ移していくつもりです。

大事にしているのは、これを“いつか作る”の願望で終わらせないこと。「いま index.html で何を意図的に捨てたか」＋「どのトリガーが来たら何を導入するか」 を、現在の決定としてセットで考えておく。それが机上の展望と、地に足のついた判断ログの違い。

まとめ

つらつらと書きましたが要は実験中・作るべき方向性の探索中の段階なので作り込むべきものが見つかるまでは作り込まないようにしているという話でした。人間がコードを書く場合だと流石に「index.html 1ファイル」縛りはしんどいですがAIに任せると割り切れれば案外こういう感じでもいけちゃうんですね。
とはいえ早く作り込むべきものを見つけてきちんとした作り込みをしたいです。

*1:手に負えなくなっている自宅の本棚をいい感じに管理したい・・・

*2:ついでにAIに任せきりだった実装内容のキャッチアップも兼ねてます

*3:NotionAIがスクショまで出してくれた

*4:人間にはだいぶ読みづらいけど。。。AIが読めれば今はヨシ

*5:AIコーディングを考えると今だったら型とかeasyさのバランスが良いGoとかKotlinあたりを選ぶかな

2025-02-08

コンピュータシステムの理論と実装のCPUエミュレータをRustとWasmで実装してブラウザで動かしてみました

コンピュータシステムの理論と実装 nand2tetris Rust Wasm SDL CPUエミュレータ

前回に引き続き今回はコンピュータシステムの理論と実装（以下、nand2tetris本）のCPUエミュレータを実装してみました。

今回のコード
概要
CPUエミュレータ部分のライブラリクレート
呼び出し元のバイナリクレート(SDLやWASM)
- SDL
- WASM
参考情報
まとめ

今回のコード

下記、タグv0.0.7になります。

github.com

下記で環境をcloneできます。

git clone -b v0.0.7 https://github.com/nihemak/nand2tetris.git
cd nand2tetris

概要

今回のCPUエミュレータは前回のハードウェアシミュレータと同様の動きをしますが実装は反対のアプローチになります。

（今回）CPUエミュレータ
- HACK言語の機械語命令の仕様からトップダウンにCPU動作を模倣するように実装
（前回）ハードウェアシミュレータ
- NAND回路からボトムアップに積み上げてHACKコンピュータのバイナリコードが動作するところを目指して実装

HACK言語の機械語命令の仕様はA命令とC命令に分かれます。

A命令	C命令
記号：@xxx バイナリ：0vvv_vvvv_vvvv_vvvv	記号：dest = comp ; jump バイナリ：111a_cccc_ccdd_djjj

A命令のアドレスはvの部分になります。

C命令のcompはバイナリaとcから判断します。

a == 0	a == 1	c	c	c	c	c	c
0	-	1	0	1	0	1	0
1	-	1	1	1	1	1	1
-1	-	1	1	1	0	1	0
D	-	0	0	1	1	0	0
A	M	1	1	0	0	0	0
!D	-	0	0	1	1	0	1
!A	!M	1	1	0	0	0	1
-D	-	0	0	1	1	1	1
-A	-M	1	1	0	0	1	1
D+1	-	0	1	1	1	1	1
A+1	M+1	1	1	0	1	1	1
D-1	-	0	0	1	1	1	0
A-1	M-1	1	1	0	0	1	0
D+A	D+M	0	0	0	0	1	0
D-A	D-M	0	1	0	0	1	1
A-D	M-D	0	0	0	1	1	1
D&A	D&M	0	0	0	0	0	0
D\|A	D\|M	0	1	0	1	0	1

C命令のdestはバイナリdから判断します。

d	d	d	compの保存先
0	0	0	null
0	0	1	M
0	1	0	D
0	1	1	DM
1	0	0	A
1	0	1	AM
1	1	0	AD
1	1	1	ADM

C命令のjumpはバイナリjから判断します。

j	j	j	jump
0	0	0	null
0	0	1	JGT
0	1	0	JEQ
0	1	1	JGE
1	0	0	JLT
1	0	1	JNE
1	1	0	JLE
1	1	1	JMP

今回の実装戦略は次のようにしました。*1

CPUエミュレータ部分をライブラリクレートとして実装
- ハードウェアシミュレータで実装したComputer構造体と関数のシグネチャを合わせる
呼び出し元のバイナリクレート(SDLやWASM)のコードをハードウェアシミュレータで実装したものから流用
- 実行方法などはハードウェアシミュレータと同じ！

CPUエミュレータ部分のライブラリクレート

ソースコードは13/cpu_emulatorです。

下記で動かせます。

cd 13/cpu_emulator/

# test all
cargo test

3つの部分から構成されています。

HACK言語の機械語命令の定義(instruction.rs)
算術演算可能なメモリ1ワード(word.rs)
エントリポイント(lib.rs)

1. HACK言語の機械語命令の定義(instruction.rs)

ソースコードは13/cpu_emulator/src/instruction.rsです。

機械語命令の定義がそのままenumで宣言的に書けて良い感じですね。

#[derive(Clone, PartialEq, Debug)]
pub enum Instruction {
    A(u16),
    C(Comp, Dest, Jump),
}

#[derive(Clone, PartialEq, Debug)]
pub enum Comp {
    Zero,       /* 0 */
    One,        /* 1 */
    MinusOne,   /* -1 */
    D,          /* D */
    A,          /* A */
    M,          /* M */
    NotD,       /* !D */
    NotA,       /* !A */
    NotM,       /* !M */
    MinusD,     /* -D */
    MinusA,     /* -A */
    MinusM,     /* -M */
    DPlusOne,   /* D+1 */
    APlusOne,   /* A+1 */
    MPlusOne,   /* M+1 */
    DMinusOne,  /* D-1 */
    AMinusOne,  /* A-1 */
    MMinusOne,  /* M-1 */
    DPlusA,     /* D+A */
    DPlusM,     /* D+M */
    DMinusA,    /* D-A */
    DMinusM,    /* D-M */
    AMinusD,    /* A-D */
    MMinusD,    /* M-D */
    DAndA,      /* D&A */
    DAndM,      /* D&M */
    DOrA,       /* D|A */
    DOrM,       /* D|M */
}

#[derive(Clone, PartialEq, Debug)]
pub enum Dest {
    Null,           /* null */
    RamA,           /* RAM[A] */
    D,              /* D */
    DAndRamA,       /* D, RAM[A] */
    A,              /* A */
    AAndRamA,       /* A, RAM[A] */
    AAndD,          /* A, D */
    AAndDAndRamA,   /* A, D, RAM[A] */
}

#[derive(Clone, PartialEq, Debug)]
pub enum Jump {
    None,                   /* none */
    GreaterThan,            /* if comp > 0 jump */
    EqualTo,                /* if comp = 0 jump */
    GreaterThanAndEqualTo,  /* if comp >= 0 jump */
    LessThan,               /* if comp < 0 jump */
    NotEqualTo,             /* if comp != 0 jump */
    LessThanAndEqualTo,     /* if comp <= 0 jump */
    True,                   /* if true jump */
}

文字列の機械語を仕様に従いデコードしています。最初にu16に変換してあとはビット判定で変換しているだけです。簡単ですね。

impl Instruction {
    pub fn new(instruction: &str) -> Self {
        let inst = Self::decode_to_binary(instruction);
        if Self::is_a_instruction(inst) {
            Self::A(inst)
        }
        else if Self::is_c_instruction(inst) {
            Self::C(
                Self::decode_c_comp(inst),
                Self::decode_c_dest(inst),
                Self::decode_c_jump(inst),
            )
        }
        else {
            panic!("error: instruction kind {:#018b}", inst);
        }
    }

    fn decode_to_binary(instruction: &str) -> u16 {
        let mut inst: u16 = 0b0000_0000_0000_0000;
        let mut bit: u16 = 0b1000_0000_0000_0000;
        for (_, c) in instruction.chars().enumerate() {
            if c == '1' { inst |= bit; }
            bit >>= 1;
        }
        inst
    }

    fn is_a_instruction(inst: u16) -> bool {
        inst & 0b1000_0000_0000_0000 == 0b0000_0000_0000_0000
    }

    fn is_c_instruction(inst: u16) -> bool {
        inst & 0b1110_0000_0000_0000 == 0b1110_0000_0000_0000
    }

    fn decode_c_comp(inst: u16) -> Comp {
        let comp = (inst & 0b0001_1111_1100_0000) >> 6;
        match comp {
            0b0_101010 => Comp::Zero,        /* 0 */
            0b0_111111 => Comp::One,         /* 1 */
            0b0_111010 => Comp::MinusOne,    /* -1 */
            0b0_001100 => Comp::D,           /* D */
            0b0_110000 => Comp::A,           /* A */
            0b1_110000 => Comp::M,           /* M */
            0b0_001101 => Comp::NotD,        /* !D */
            0b0_110001 => Comp::NotA,        /* !A */
            0b1_110001 => Comp::NotM,        /* !M */
            0b0_001111 => Comp::MinusD,      /* -D */
            0b0_110011 => Comp::MinusA,      /* -A */
            0b1_110011 => Comp::MinusM,      /* -M */
            0b0_011111 => Comp::DPlusOne,    /* D+1 */
            0b0_110111 => Comp::APlusOne,    /* A+1 */
            0b1_110111 => Comp::MPlusOne,    /* M+1 */
            0b0_001110 => Comp::DMinusOne,   /* D-1 */
            0b0_110010 => Comp::AMinusOne,   /* A-1 */
            0b1_110010 => Comp::MMinusOne,   /* M-1 */
            0b0_000010 => Comp::DPlusA,      /* D+A */
            0b1_000010 => Comp::DPlusM,      /* D+M */
            0b0_010011 => Comp::DMinusA,     /* D-A */
            0b1_010011 => Comp::DMinusM,     /* D-M */
            0b0_000111 => Comp::AMinusD,     /* A-D */
            0b1_000111 => Comp::MMinusD,     /* M-D */
            0b0_000000 => Comp::DAndA,       /* D&A */
            0b1_000000 => Comp::DAndM,       /* D&M */
            0b0_010101 => Comp::DOrA,        /* D|A */
            0b1_010101 => Comp::DOrM,        /* D|M */
            _ => panic!("error: comp {:#018b}", comp),
        }
    }

    fn decode_c_dest(inst: u16) -> Dest {
        let dest = (inst & 0b0000_0000_0011_1000) >> 3;
        match dest {
            0b000 => Dest::Null,            /* null */
            0b001 => Dest::RamA,            /* RAM[A] */
            0b010 => Dest::D,               /* D */
            0b011 => Dest::DAndRamA,        /* D, RAM[A] */
            0b100 => Dest::A,               /* A */
            0b101 => Dest::AAndRamA,        /* A, RAM[A] */
            0b110 => Dest::AAndD,           /* A, D */
            0b111 => Dest::AAndDAndRamA,    /* A, D, RAM[A] */
            _ => panic!("error: dest {:#018b}", dest),
        }
    }

    fn decode_c_jump(inst: u16) -> Jump {
        let jump = inst & 0b0000_0000_0000_0111;
        match jump {
            0b000 => Jump::None,                    /* none */
            0b001 => Jump::GreaterThan,             /* if comp > 0 jump */
            0b010 => Jump::EqualTo,                 /* if comp = 0 jump */
            0b011 => Jump::GreaterThanAndEqualTo,   /* if comp >= 0 jump */
            0b100 => Jump::LessThan,                /* if comp < 0 jump */
            0b101 => Jump::NotEqualTo,              /* if comp != 0 jump */
            0b110 => Jump::LessThanAndEqualTo,      /* if comp <= 0 jump */
            0b111 => Jump::True,                    /* if true jump */
            _ => panic!("error: jump {:#018b}", jump),
        }
    }
}

2. 算術演算可能なメモリ1ワード(word.rs)

ソースコードは13/cpu_emulator/src/word.rsです。

基本的にRust組み込みの算術演算が使えるのですがi16にすると最上位ビットをONにできなかったりNOT演算がうまく動作しないなど不都合があります。*2そのため専用の構造体を定義しました。内部でu16を保持し符号付き整数を2の補数で表現し算術演算をエミュレートしています。オーバーフローも許容するようにしてます。i16の再実装みたいな感じですね。

今回は演算子オーバーロードして演算子で使えるようにしてみました。

#[derive(Clone, Debug, Copy)]
pub struct Word {
    value: u16,
}

impl fmt::Display for Word {
    fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result {
        write!(f, "{}", self.value)
    }
}

impl fmt::Binary for Word {
    fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result {
        write!(f, "{:#018b}", self.value)
    }
}

impl Word {
    pub fn new() -> Self {
        Word { value: 0b0000_0000_0000_0000 }
    }

    pub fn from(value: u16) -> Self {
        Word { value }
    }

    pub fn to_u16(&self) -> u16 {
        self.value
    }

    pub fn to_i16(&self) -> i16 {
        if self.value & 0b1000_0000_0000_0000 == 0 {
            self.value as i16
        }
        else {
            -((!self.value).wrapping_add(0b0000_0000_0000_0001) as i16)
        }
    }
}

impl ops::Not for Word {
    type Output = Self;

    fn not(self) -> Self::Output {
        Word {
            value: !self.value
        }
    }
}

impl ops::BitAnd for Word {
    type Output = Self;

    fn bitand(self, rhs: Self) -> Self::Output {
        Word {
            value: self.value & rhs.value
        }
    }
}

impl ops::BitOr for Word {
    type Output = Self;

    fn bitor(self, rhs: Self) -> Self::Output {
        Word {
            value: self.value | rhs.value
        }
    }
}

impl ops::Add for Word {
    type Output = Self;

    fn add(self, other: Self) -> Self {
        Word {
            value: self.value.wrapping_add(other.value)
        }
    }
}

impl ops::Neg for Word {
    type Output = Self;

    fn neg(self) -> Self::Output {
        Word {
            value: (!self.value).wrapping_add(0b0000_0000_0000_0001)
        }
    }
}


impl ops::Sub for Word {
    type Output = Self;

    fn sub(self, other: Self) -> Self::Output {
        self + -other
    }
}

3. エントリポイント(lib.rs)

ソースコードは13/cpu_emulator/src/lib.rsです。

ライブラリクレートの定義です。ハードウェアシミュレータで実装したComputer構造体と関数のシグネチャを合わせています。

呼び出し元は次のようになる想定です。

load_programで機械語ソースコード(文字列の機械語の列)を読み込んでInstructionにデコードしromにセット
呼び出し元で次を無限ループ
1. 押下中のキーコードを取得
2. stepを呼び出すとpc(プログラムカウンタ)に従い1step処理が進む
3. get_screenまたはget_update_screen_pixelsで画面の状態を取得し描画

stepではInstructionに従った処理をしているだけです。 get_screenはSCREENメモリ全て、get_update_screen_pixelsは前回呼び出し以降に更新のあったピクセルのみ、それぞれ取得できます。後者だと描画数を抑えることができます。

#[derive(Clone)]
pub struct Computer {
    pc: Word,
    a: Word,
    d: Word,
    ram: Vec<Word>,
    rom: Vec<Instruction>,
    update_screen_addrs: Vec<u16>,
}

impl Computer {
    pub fn new() -> Self {
        Computer {
            pc: Word::new(),
            a: Word::new(),
            d: Word::new(),
            ram: Vec::new(),
            rom: Vec::new(),
            update_screen_addrs: Vec::new(),
        }
    }

    pub fn load_program(&mut self, instructions: Vec<&str>) {
        self.rom.clear();
        for instruction in instructions {
            self.rom.push(Instruction::new(instruction));
        }
    }

    pub fn step(&mut self, reset: bool, key_code: u16) {
        if reset {
            self.reset_ram();
            self.pc = Word::new();
        }

        self.ram[24576 /* KBD */] = Word::from(key_code);

        let inst = &self.rom[self.pc.to_u16() as usize];
        match inst {
            Instruction::A(a) => {
                self.a = Word::from(*a);
                self.pc = self.pc + Word::from(1);
            },
            Instruction::C(comp, dest, jump) => {
                let m = self.ram[self.a.to_u16() as usize];
                let comp: Word = Self::comp(comp, &self.a, &self.d, &m);

                match dest {
                    InstructionCDest::Null          => { }, /* null */
                    InstructionCDest::RamA          => {    /* RAM[A] */
                        self.ram[self.a.to_u16() as usize] = comp;
                        if Self::is_screen_addr(&self.a) {
                            self.update_screen_addrs.push(self.a.to_u16());
                        }
                    },
                    InstructionCDest::D             => {    /* D */
                        self.d = comp;
                    },
                    InstructionCDest::DAndRamA      => {    /* D, RAM[A] */
                        self.d = comp;
                        self.ram[self.a.to_u16() as usize] = comp;
                        if Self::is_screen_addr(&self.a) {
                            self.update_screen_addrs.push(self.a.to_u16());
                        }
                    },
                    InstructionCDest::A             => {    /* A */
                        self.a = comp;
                    }, 
                    InstructionCDest::AAndRamA      => {    /* A, RAM[A] */
                        self.a = comp;
                        self.ram[self.a.to_u16() as usize] = comp;
                        if Self::is_screen_addr(&self.a) {
                            self.update_screen_addrs.push(self.a.to_u16());
                        }
                    },
                    InstructionCDest::AAndD         => {    /* A, D */
                        self.a = comp;
                        self.d = comp;
                    },
                    InstructionCDest::AAndDAndRamA  => {    /* A, D, RAM[A] */
                        self.a = comp;
                        self.d = comp;
                        self.ram[self.a.to_u16() as usize] = comp;
                        if Self::is_screen_addr(&self.a) {
                            self.update_screen_addrs.push(self.a.to_u16());
                        }
                    },
                }
                println!("pc {}, a {:#018b}, d {:#018b}, comp {}", self.pc, self.a, self.d, comp);

                self.pc = if Self::jump(jump, &comp) { self.a.clone() } else { self.pc + Word::from(1) };
            },
        }
    }

    fn reset_ram(&mut self) {
        self.ram.clear();
        for _ in 0..65535 {
            self.ram.push(Word::new());
        }
    }

    fn is_screen_addr(addr: &Word) -> bool {
        let addr = addr.to_u16();
        addr >= 16384 /* SCREEN */ && addr <= 24575
    }

    fn comp(comp: &InstructionCComp, a: &Word, d: &Word, m: &Word) -> Word {
        match comp {
            InstructionCComp::Zero      => Word::new(),             /* 0 */
            InstructionCComp::One       => Word::from(1),           /* 1 */
            InstructionCComp::MinusOne  => -Word::from(1),          /* -1 */
            InstructionCComp::D         => d.clone(),               /* D */
            InstructionCComp::A         => a.clone(),               /* A */
            InstructionCComp::M         => m.clone(),               /* M */
            InstructionCComp::NotD      => !(*d),                   /* !D */
            InstructionCComp::NotA      => !(*a),                   /* !A */
            InstructionCComp::NotM      => !(*m),                   /* !M */
            InstructionCComp::MinusD    => -(*d),                   /* -D */
            InstructionCComp::MinusA    => -(*a),                   /* -A */
            InstructionCComp::MinusM    => -(*m),                   /* -M */
            InstructionCComp::DPlusOne  => (*d) + Word::from(1),    /* D+1 */
            InstructionCComp::APlusOne  => (*a) + Word::from(1),    /* A+1 */
            InstructionCComp::MPlusOne  => (*m) + Word::from(1),    /* M+1 */
            InstructionCComp::DMinusOne => (*d) - Word::from(1),    /* D-1 */
            InstructionCComp::AMinusOne => (*a) - Word::from(1),    /* A-1 */
            InstructionCComp::MMinusOne => (*m) - Word::from(1),    /* M-1 */
            InstructionCComp::DPlusA    => (*d) + (*a),             /* D+A */
            InstructionCComp::DPlusM    => (*d) + (*m),             /* D+M */
            InstructionCComp::DMinusA   => (*d) - (*a),             /* D-A */
            InstructionCComp::DMinusM   => (*d) - (*m),             /* D-M */
            InstructionCComp::AMinusD   => (*a) - (*d),             /* A-D */
            InstructionCComp::MMinusD   => (*m) - (*d),             /* M-D */
            InstructionCComp::DAndA     => (*d) & (*a),             /* D&A */
            InstructionCComp::DAndM     => (*d) & (*m),             /* D&M */
            InstructionCComp::DOrA      => (*d) | (*a),             /* D|A */
            InstructionCComp::DOrM      => (*d) | (*m),             /* D|M */
        }
    }

    fn jump(jump: &InstructionCJump, comp: &Word) -> bool {
        match jump {
            InstructionCJump::None                  => { false },               /* none */
            InstructionCJump::GreaterThan           => { comp.to_i16() >  0 },  /* if comp > 0 jump */
            InstructionCJump::EqualTo               => { comp.to_i16() == 0 },  /* if comp = 0 jump */
            InstructionCJump::GreaterThanAndEqualTo => { comp.to_i16() >= 0 },  /* if comp >= 0 jump */
            InstructionCJump::LessThan              => { comp.to_i16() <  0 },  /* if comp < 0 jump */
            InstructionCJump::NotEqualTo            => { comp.to_i16() != 0 },  /* if comp != 0 jump */
            InstructionCJump::LessThanAndEqualTo    => { comp.to_i16() <= 0 },  /* if comp <= 0 jump */
            InstructionCJump::True                  => { true },                /* if true jump */
        }
    }

    pub fn get_screen(&self) -> [bool; 131072] {
        let mut screen = [false; 131072];
        let mut x = 0;
        for i in 0..8192 {
            let word = self.ram[16384 /* SCREEN */ + i].to_u16();
            let mut bit: u16 = 0b0000_0000_0000_0001;
            for _ in 0..16 {
                if word & bit != 0 {
                    screen[x] = true;
                }
                bit <<= 1;
                x += 1;
            }
        }
        screen
    }

    pub fn get_update_screen_pixels(&mut self) -> Vec<(i32, i32, bool)> {
        let mut pixels = Vec::new();
        for addr in &self.update_screen_addrs {
            let base = (addr - 16384 /* SCREEN */) * 16;
            let word = self.ram[*addr as usize].to_u16();
            let mut bit: u16 = 0b0000_0000_0000_0001;
            for i in 0..16 {
                let px: i32 = (base + i).into();
                let x: i32 = px % 512;
                let y: i32 = px / 512;
                let color = word & bit != 0;
                pixels.push((x, y, color));
                bit <<= 1;
            }
        }
        self.update_screen_addrs.clear();
        pixels
    }
}

呼び出し元のバイナリクレート(SDLやWASM)

ハードウェアシミュレータで実装したものから流用してます。

SDL

ソースコードは13/cpu_emulator_sdlです。

下記で動かせます。

cd 13/cpu_emulator_sdl/

# test all
cargo test

# execute
cargo run

# execute (release build)
cargo build --release
./target/release/cpu_emulator_sdl

コードも実行結果もハードウェアシミュレータとほぼ変わりません。

WASM

ソースコードは13/cpu_emulator_wasmです。

下記で動かせます。

cd 13/cpu_emulator_sdl/

# test all
cargo test

nvm i v14.15.1
npm --version
# 6.14.8
node --version
# v14.15.1

npm install
npm start

コードも実行結果もハードウェアシミュレータとほぼ変わりません。

参考情報

下記の書籍は少し参考にしました。

gihyo.jp

3章でC言語による簡単なCPUエミュレータの実装がソースコード付きで説明されてます。

book.mynavi.jp

2.3でC言語による簡単なx86 エミュレータの実装がソースコード付きで説明されてます。

まとめ

ハードウェアシミュレータに比べると記述も少なく仕様をそのまま実装するだけだったのでかなり楽でした。ただ実行スピードは遅いです。*3 シンプルな実装で特に時間がかかるような変なこともしていないはずなのでどこか根本的な部分での見落とし、ボトルネックが存在しそうな気がします。暇があれば解消したいです。

*1:ハードウェアシミュレータの実装も同様にライブラリクレートに共通化しSDLとWASMのバイナリクレートから利用する形にリファクタリングしています。詳細はソースコード参照

*2:例えば、「let foo: i16 = 0b1010_1010_1010_1010;」は「error: literal out of range for i16」になります。

*3:それでもハードウェアシミュレータの実行スピードに比べれば幾分マシですが、実用に耐えないレベルです

2024-12-24

コンピュータシステムの理論と実装のハードウェアシミュレータをRustとWasmで実装してブラウザで動かしてみました

コンピュータシステムの理論と実装 nand2tetris Rust Wasm SDL ハードウェアシミュレータ

これはドクターメイト Advent Calendar 2024の24日目です。

クリスマスイブですね、クリスマスは楽しく過ごしたいなと思う今日この頃です。さて、せっかくRustの会社にいるしRustキャッチアップしたいなぁと思って*1Rustでコンピュータシステムの理論と実装（以下、nand2tetris本）*2のハードウェアシミュレータを実装してみました。空気も読まずにプログラマらしくちゃんと動くものを実装してみた系のテーマにしたらだいぶ時間を費やすことになりました。自分向けの備忘録でもあるので以下ダラダラと長くなっています。*3

以前のブログ記事では書籍1〜5章のハードウェアパーツのロジックをHDLで実装し書籍が用意したハードウェアシミュレータ上で実行しました。今回はRustでハードウェアシミュレータもろともフルスクラッチで全て実装します。以前に書いた1〜5章のブログ記事は下記ですね。

nihemak.hatenablog.com

今回のコード
概要
ステップ1: RustとSDLによる実装
ステップ2: RustとWasmによる実装
ステップ3: RustとWasmによる実装（ビルトイン版）
- ビルトイン版のイメージ
- 実装を終えて
まとめ

今回のコード

下記、タグv0.0.6になります。

github.com

下記で環境をcloneできます。

git clone -b v0.0.6 https://github.com/nihemak/nand2tetris.git
cd nand2tetris

概要

今回は冒頭で書いた通りRustでNANDゲートの関数を定義するところから始めてHACKコンピュータのバイナリコードが動作するところを目指して実装していきました。この記事の最後にはブラウザで動くところまでは辿り着けます。ただ最初にネタバレすると実用的な動作速度には達していません。ご容赦くださいませ。

実装は次のステップで行いました。

ステップ1: RustとSDLによる実装
- ハードウェア実装に集中するためまずはScreenとKeyboardをSDLで実装
ステップ2: RustとWasmによる実装
- SDLをWasmに置き換えてブラウザで動くように実装
ステップ3: RustとWasmによる実装（ビルトイン版）
- ハードウェア実装を最適化コード（Nand由来ではないズルコード）に置き換えて動作速度を改善

全体構成はこんな感じです。

ステップ1: RustとSDLによる実装

まずScreenやKeyboardをSDL（Simple DirectMedia Layer）で実現する構成でハードウェアシミュレータを実装しました。

13/HardwareSimulatorです。詳細はコードを参照して下さい。

下記で動かせます。（事前にSDL2をインストールしておく必要があります。自分はmacなので brew install sdl2 しました。）

cd 13/HardwareSimulator

# test all
# https://stackoverflow.com/questions/74637159/how-to-increase-stack-size-of-threads-used-by-cargo-test
RUST_MIN_STACK=3000000 cargo test

# execute
cargo run

# execute (release build)
cargo build --release
./target/release/HardwareSimulator

起動すると画面（ウインドウ）を白から黒に塗り替えていきます。Escキーで終了します。

ブール論理

1章のブール論理の実装は13/HardwareSimulator/src/boolean_logic.rsです。対応するHDLの実装は01にあります。

下記のように0と1はbool型にしました。型名はbitです。falseが0、trueが1ですね。nand関数から初めてその他のゲートも関数として定義しています。

pub type bit = bool;
pub type word = [bit; 16];

pub fn nand(a: bit, b: bit) -> bit {
    !(a && b)
}

pub fn not(a: bit) -> bit {
    nand(a, a)
}

pub fn and(a: bit, b: bit) -> bit {
    not(nand(a, b))
}

//...

テストもちゃんと書くようにしました。HDLの*.tstのテストコードを参考にしています。パラメタライズドテストにするためにrstestを使っています。

#[cfg(test)]
mod tests {
    use rstest::*;
    use super::*;

    #[rstest]
    #[case((false, false), true)]
    #[case((false, true),  true)]
    #[case((true,  false), true)]
    #[case((true,  true),  false)]
    fn test_nand(#[case] input: (bit, bit), #[case] output: bit) {
        let (a, b) = input;
        assert_eq!(output, nand(a, b));
    }

//...

あとtrue, falseの羅列はしんどいのでu16からwordに変換するu16_to_word関数などヘルパー関数を定義して読み書きを楽にする工夫もしました。

    #[rstest]
    #[case(u16_to_word(0b0000_0000_0000_0000), u16_to_word(0b1111_1111_1111_1111))]
    #[case(u16_to_word(0b1111_1111_1111_1111), u16_to_word(0b0000_0000_0000_0000))]
    #[case(u16_to_word(0b1010_1010_1010_1010), u16_to_word(0b0101_0101_0101_0101))]
    #[case(u16_to_word(0b0011_1100_1100_0011), u16_to_word(0b1100_0011_0011_1100))]
    #[case(u16_to_word(0b0001_0010_0011_0100), u16_to_word(0b1110_1101_1100_1011))]
    fn test_not16(#[case] input: word, #[case] output: word) {
        assert_eq!(output, not16(input));
    }

ヘルパー関数は13/HardwareSimulator/src/helper.rsです。

ブール算術

2章のブール算術の実装は13/HardwareSimulator/src/boolean_arithmetic.rsです。対応するHDLの実装は02にあります。

こちらも愚直にゲートの関数を定義していってます。テストもちゃんと書いてます。

pub fn half_adder(a: bit, b: bit) -> (bit, bit) {
    let sum = xor(a, b);
    let carry = and(a, b);
    (sum, carry)
}

pub fn full_adder(a: bit, b: bit, c: bit) -> (bit, bit) {
    let (sum0, carry0) = half_adder(a, b);
    let (sum, carry1) = half_adder(sum0, c);
    let carry = or(carry0, carry1);
    (sum, carry)
}

//...

順序回路

3章の順序回路の実装は13/HardwareSimulator/src/sequential_circuit.rsです。対応するHDLの実装は03にあります。

こちらも愚直な回路の定義です。クロックはbitにしました。時間の概念が入ってきてここから若干複雑になってきます。テストが重要になってきます*4。

#[derive(Debug, Copy, Clone)]
pub struct DFF {
    past_bit: bit,
    new_bit: bit
}

impl DFF {
    pub fn new() -> Self {
        DFF {
            past_bit: false,
            new_bit: false
        }
    }

    pub fn update(&mut self, clk: bit, a: bit) {
        if clk {
            self.past_bit = self.new_bit;
            self.new_bit = a
        }
    }

    pub fn get(self, clk: bit) -> bit {
        if clk { self.past_bit } else { self.new_bit }
    }
}

//...

コンピュータアーキテクチャ

5章のコンピュータアーキテクチャの実装は13/HardwareSimulator/src/hardware.rsです。対応するHDLの実装は05にあります。

あと少しです。ScreenやKeyboard、ROM32Kなどの実装は書籍にはなかったので考慮が必要になります。アウトプットが再度インプットになる回路などだいぶハマりましたがテストが通っているので多分大丈夫なはず。知らんけど。

Screen

今回は画面の情報を取得できるget_all関数を用意し描画の責務を呼び出し元が持つ設計にしました。後からUIをWasmに置き換えることも考慮した結果です。

基本、RAM4Kの読み書きになるのですが動かしたら動作が激重だったのでget_all関数はRAM4Kを使わないビルトインの処理にするズルをしています。RAM4Kを使うロジックはコメントアウトで残してあります。

#[derive(Copy, Clone)]
pub struct Screen {
    rams: [RAM4K; 2],
    screen: [bit; 131072],
}

impl Screen {
    pub fn new() -> Self {
        Screen { 
            rams: [RAM4K::new(); 2],
            screen: [false; 131072],
        }
    }

    fn update(&mut self, clk: bit, input: word, load: bit, address: [bit; 13]) {
        let (a, b) = dmux(load, address[12]);
        let address_low = bit13_to_bit12(address);
        self.rams[0].update(clk, input, a, address_low);
        self.rams[1].update(clk, input, b, address_low);

        if load {
            let address_num = bit13_to_u16(address);
            if address_num <= 24575 {
                let screen_address: u32 = 16 * (address_num as u32);
                for n in 0..16 {
                    self.screen[(screen_address + n) as usize] = input[n as usize];
                }
            }
        }
    }

    fn get(&self, clk: bit, address: [bit; 13]) -> word {
        let address_low = bit13_to_bit12(address);
        mux16(
            self.rams[0].get(clk, address_low),
            self.rams[1].get(clk, address_low),
            address[12]
        )
    }

    pub fn get_all(&self) -> [bit; 131072] {
        // let mut screen = [false; 131072];
        // let mut x = 0;
        // for i in 0..8192 {
        //     let address = u16_to_13bit(i);
        //     let word = self.get(false, address);
        //     for j in 0..16 {
        //         screen[x] = word[j];
        //         x += 1;
        //     }
        // }
        // screen
        self.screen
    }
}

Keyboard

KeyboardもScreenと同様に押下キーの取得の責務を呼び出し元でする設計になってます。そのためupdate関数で指定されたキーコードを保持するだけになってます。

#[derive(Debug, Copy, Clone)]
pub struct Keyboard {
    key_code: Register,
}

impl Keyboard {
    pub fn new() -> Self {
        Keyboard { key_code: Register::new() }
    }

    fn update(&mut self, clk: bit, key_code: word) {
        self.key_code.update(clk, key_code, true);
    }

    fn get(&self, clk: bit) -> word {
        self.key_code.get(clk)
    }
}

ROM32K

ROM32KはRAM4Kの読み書きだけです。HACKのバイナリコードを読み込むload関数を用意し呼び出し元で指定する設計にしました。*.hackをそのまま読み込めるように（逆順に）デコードして読み込むようにしてあります。

#[derive(Copy, Clone)]
pub struct ROM32K {
    rams: [RAM4K; 8]
}

impl ROM32K {
    pub fn new() -> Self {
        ROM32K {
            rams: [RAM4K::new(); 8]
        }
    }

    pub fn update(&mut self, clk: bit, input: word, address: [bit; 15]) {
        let address_low = bit15_to_bit12(address);
        let address_high = [address[12], address[13], address[14]];
        let (a, b, c, d, e, f, g, h) = dmux8way(true, address_high);
        self.rams[0].update(clk, input, a, address_low);
        self.rams[1].update(clk, input, b, address_low);
        self.rams[2].update(clk, input, c, address_low);
        self.rams[3].update(clk, input, d, address_low);
        self.rams[4].update(clk, input, e, address_low);
        self.rams[5].update(clk, input, f, address_low);
        self.rams[6].update(clk, input, g, address_low);
        self.rams[7].update(clk, input, h, address_low);
    }

    fn get(&self, clk: bit, address: [bit; 15]) -> word {
        let address_low = bit15_to_bit12(address);
        let address_high = [address[12], address[13], address[14]];
        mux8way16(
            self.rams[0].get(clk, address_low),
            self.rams[1].get(clk, address_low),
            self.rams[2].get(clk, address_low),
            self.rams[3].get(clk, address_low),
            self.rams[4].get(clk, address_low),
            self.rams[5].get(clk, address_low),
            self.rams[6].get(clk, address_low),
            self.rams[7].get(clk, address_low),
            address_high
        )
    }

    pub fn load(&mut self, instructions: Vec<&str>) {
        let mut counter = u16_to_word(0b0000000000000000);
        for instruction in instructions {
            let mut decorded_instruction = u16_to_word(0b0000000000000000);
            for (i, c) in instruction.chars().enumerate() {
                if c == '1' {
                    decorded_instruction[15 - i] = true;
                }
            }
            // println!("instruction: {}", word_to_u16(decorded_instruction));
    
            let address = word_to_bit15(counter);
            self.update(true, decorded_instruction, address);
            counter = add16(counter, u16_to_word(0b0000000000000001));
        }
    }
}

main（エントリポイント）

エントリポイントの実装は13/HardwareSimulator/src/main.rsです。

下記をやってます。

ここまで作ったコンピュータにHACKのバイナリコードを読み込んで起動
無限ループ
1. Escが押下されたら終了
2. 押下されたキーコードを取得しコンピュータを1クロック（true, false）進める
3. コンピュータの画面情報を取得し描画

1. コンピュータに読み込むHACKのバイナリコード

ファイル等から読み込めたらかっこいいのですが今回はソースコード内に命令列を決め打ちしてあります。内容は04/fill/Fill.asmのデフォルトを背景黒にしたバージョンです。実行すると最初に画面を真っ黒にして何かキーが押下されたら画面を真っ白にします。*5

    // Fill
    let instructions: Vec<&str> = vec![
                            //(LOOP_KBD)
        "0110000000000000", //        @KBD
        "1111110000010000", //        D=M
        "0000000000001000", //        @SELECT_BLACK
        "1110001100000010", //        D; JEQ
        "0000000000000000", //        @0
        "1110110000010000", //        D=A
        "0000000000001010", //        @SET_COLOR
        "1110101010000111", //        0; JMP
                            //(SELECT_BLACK)
        "0000000000000000", //        @0
        "1110110010010000", //        D=A-1
                            //(SET_COLOR)
        "0000000000010000", //        @color
        "1110001100001000", //        M=D

        "0100000000000000", //        @SCREEN
        "1110110000010000", //        D=A
        "0000000000010001", //        @pos
        "1110001100001000", //        M=D

                            //        // 32 * 256 = 8192
        "0010000000000000", //        @8192
        "1110110000010000", //        D=A
        "0000000000010010", //        @n
        "1110001100001000", //        M=D

                            //(LOOP_FILL)
        "0000000000010010", //        @n
        "1111110000010000", //        D=M
        "0000000000100011", //        @FILL_END
        "1110001100000010", //        D; JEQ

                            //        // print color
        "0000000000010000", //        @color
        "1111110000010000", //        D=M
        "0000000000010001", //        @pos
        "1111110000100000", //        A=M
        "1110001100001000", //        M=D

        "0000000000010001", //        @pos
        "1111110111001000", //        M=M+1
        "0000000000010010", //        @n
        "1111110010001000", //        M=M-1

        "0000000000010100", //        @LOOP_FILL
        "1110101010000111", //        0; JMP
                            //(FILL_END)
        "0000000000000000", //        @LOOP_KBD
        "1110101010000111", //        0; JMP

    ];

2-2. 押下されたキーコードの取得

get_keyboard_press_code関数でしてます。SDLで押下判定してキーコードへのマッピングするのみです。

fn get_keyboard_press_code(keystate: &KeyboardState) -> word {
    u16_to_word(
        if keystate.is_scancode_pressed(Scancode::Num0)  { 0b0000_0000_0011_0000 } else
        if keystate.is_scancode_pressed(Scancode::Num1)  { 0b0000_0000_0011_0001 } else
        if keystate.is_scancode_pressed(Scancode::Num2)  { 0b0000_0000_0011_0010 } else
        if keystate.is_scancode_pressed(Scancode::Num3)  { 0b0000_0000_0011_0011 } else
        if keystate.is_scancode_pressed(Scancode::Num4)  { 0b0000_0000_0011_0100 } else
        if keystate.is_scancode_pressed(Scancode::Num5)  { 0b0000_0000_0011_0101 } else
        if keystate.is_scancode_pressed(Scancode::Num6)  { 0b0000_0000_0011_0110 } else
        if keystate.is_scancode_pressed(Scancode::Num7)  { 0b0000_0000_0011_0111 } else
// ...

2-2. コンピュータを1クロック進める

1クロック進むComputerのstep関数を呼び出します。

        let state = event_pump.keyboard_state();
        computer.step(reset, get_keyboard_press_code(&state));
        reset = false;

Computerのstep関数はこちらです。

    pub fn step(&mut self, reset: bit, word: word) {
        let mut clk = true;
        self.update(clk, reset, word);
        clk = !clk;
        self.update(clk, reset, word);
    }

2-3. コンピュータの画面情報を取得し描画

display_screen関数でしてます。Screenのget_all関数の結果をSDLで描画しているだけです。

fn display_screen(canvas: &mut WindowCanvas, computer: &Computer) {
    let screen = computer.get_screen();
    for px in 0..screen.len() {
        let x = px % 512;
        let y = px / 512;
        let color = if screen[px] { Color::RGB(0, 0, 0) } else { Color::RGB(255, 255, 255) };
        canvas.set_draw_color(color);
        let w = 2;
        canvas.fill_rect(Rect::new((x * w).try_into().unwrap(), (y * w).try_into().unwrap(), w as u32, w as u32)).unwrap();
    }
}

実装を終えて

正直、デバッグも難しくて実装はしんどかったです。いくつかトピックを紹介します。

cargo testでスタックサイズが足りないエラーになる

13/HardwareSimulator/README.mdの通りテストはデフォルトだと fatal runtime error: stack overflow になり途中で止まります。これは巨大な構造体を全てスタックに置いているためです。ヒープに置くようにすれば解消するかもですが後回しにしました。

# test all
# https://stackoverflow.com/questions/74637159/how-to-increase-stack-size-of-threads-used-by-cargo-test
RUST_MIN_STACK=3000000 cargo test

doc.rust-jp.rs

動作速度が遅い

プログラムを起動すると画面がすぐに真っ黒になるはずなのですが全然なりません。。画面上部からちょっとずつ黒く塗りつぶしされていくのを眺めるしかないです。速度改善をしていかないと使い物にならなそうです。

参考にした情報源

今回は第1版です。

www.oreilly.co.jp

NANDゲートからのハードウェアシミュレータを実装する部分はハマったとき下記を参考にさせていただきました。

zenn.dev

github.com

caddi.tech

SDLの実装部分は下記を参考にさせていただきました。

qiita.com

ステップ2: RustとWasmによる実装

実行速度が出ないとはいえ一応は動いたので次のステップとしてSDLの部分をWasm化しました。RustとWebAssemblyによるゲーム開発の1〜3章の内容を参考にしました。*6

13/HardwareSimulatorWasmです。詳細はコードを参照して下さい。

下記で動かせます。

cd 13/HardwareSimulatorWasm

# test all
TEST=1 RUST_MIN_STACK=3000000 cargo test

nvm i v14.15.1
npm --version
# 6.14.8
node --version
# v14.15.1

npm install
npm start

起動すると画面（ブラウザ）を白から黒に塗り替えていきます。

ハードウェア部分の実装

13/HardwareSimulatorのハードウェア部分の実装を13/HardwareSimulatorWasm/src/nand2tetrisにコピーして調整しました。ロジックは変更していないです。

SDL実装のmainにあたる部分の実装

13/HardwareSimulatorWasm/src/nand2tetris.rsにあります。

キーボードや画面描画のコードはWasm向けに変更しています。

キーボードはこんな感じ。SDL実装とロジックは同じです。

    fn get_keyboard_press_code(keystate: &KeyState) -> word {
        u16_to_word(
            if keystate.is_pressed("Digit0")     { 0b0000_0000_0011_0000 } else 
            if keystate.is_pressed("Digit1")     { 0b0000_0000_0011_0001 } else 
            if keystate.is_pressed("Digit2")     { 0b0000_0000_0011_0010 } else 
            if keystate.is_pressed("Digit3")     { 0b0000_0000_0011_0011 } else 
            if keystate.is_pressed("Digit4")     { 0b0000_0000_0011_0100 } else 
            if keystate.is_pressed("Digit5")     { 0b0000_0000_0011_0101 } else 
            if keystate.is_pressed("Digit6")     { 0b0000_0000_0011_0110 } else 
            if keystate.is_pressed("Digit7")     { 0b0000_0000_0011_0111 } else 
            if keystate.is_pressed("Digit8")     { 0b0000_0000_0011_1000 } else 
            if keystate.is_pressed("Digit9")     { 0b0000_0000_0011_1001 } else 
            if keystate.is_pressed("ArrowLeft")  { 0b0000_0000_1000_0010 } else 
// ...

画面描画はこんな感じ。こちらもSDL実装とロジックは同じですね。

    fn draw(&self, renderer: &Renderer) {
        let screen = self.computer.get_screen();
        for px in 0..screen.len() {
            let x = px % 512;
            let y = px / 512;
            let color = if screen[px] {"#000000"} else {"#FFFFFF"};
            renderer.draw_pixel(color, x.try_into().unwrap(), y.try_into().unwrap());
        }
    }

Wasm向けのコード

下記です。ここはRustとWebAssemblyによるゲーム開発の1〜3章の内容の通りです。

13/HardwareSimulatorWasm/src/lib.rs
- エントリポイント
13/HardwareSimulatorWasm/src/browser.rs
- ブラウザコード
13/HardwareSimulatorWasm/src/engine.rs
- 書籍のゲームエンジンにあたるコード

実装を終えて

無事にWasmで動いてホッとしました。いくつかトピックを紹介します。

nodeバージョンが新しいとエラーになる

RustとWebAssemblyによるゲーム開発のコードが古いせいかNode.js v22.6.0だとnpm startでエラーになります。仕方がないので13/HardwareSimulatorWasm/README.mdの通り古いバージョンにして動かしました。最新バージョンに対応させたいですね。

nvm i v14.15.1
npm --version
# 6.14.8
node --version
# v14.15.1

npm install
npm start

ブラウザでスタックサイズが足りないエラーになる

npm start するとブラウザで RuntimeError: memory access out of bounds になり途中で止まりました。cargo testで起きるエラーと同じですね。仕方がないので13/HardwareSimulatorWasm/build.rsの通り起動時にスタックサイズを増やして回避しました。cargo testだと邪魔になるので環境変数でTESTを指定されなかった場合だけ動くようにしてます。カッコ悪いので直したいですね。

use std::env;

fn main() {
    // FIXME: Remove this
    if let Ok(val) = env::var("TEST") {
    } else {
        // https://doc.rust-jp.rs/rust-by-example-ja/cargo/build_scripts.html
        // https://github.com/rustwasm/wasm-bindgen/issues/3368#issuecomment-1483954797
        // https://github.com/aduros/wasm4/blob/main/cli/assets/templates/rust/.cargo/config.toml
        // https://doc.rust-jp.rs/rust-by-example-ja/std/box.html
        println!("cargo::rustc-link-arg=-zstack-size=6000000");
    }
}

build.rsは13/HardwareSimulatorWasm/Cargo.tomlで指定してます。

build = "build.rs"

doc.rust-jp.rs

13/HardwareSimulatorWasm/README.mdの通りcargo testでTEST=1を指定する必要があります。

# test all
TEST=1 RUST_MIN_STACK=3000000 cargo test

UI部分をSDLからWasmに変えるだけでほぼOKだった

ハードウェア部分の実装はほぼ変えないで良かったです。Wasm実装もほぼRustとWebAssemblyによるゲーム開発の内容でできたので比較的楽な対応でした。

やっぱり速度が出ない

SDL実装よりも遅いです。。ブラウザで動かすのでしょうがないと思いますが。

参考にした情報源

この書籍をがっつり参考にしました。

www.oreilly.co.jp

書籍のソースコードも参考にしました。

github.com

ステップ3: RustとWasmによる実装（ビルトイン版）

流石に遅いので高速化のためにRust組み込みのビット演算などを使った最適化版（ズルコード版）のビルトイン版も実装してどの程度の高速化になるか試してみました。

13/HardwareSimulatorWasmBuiltInです。詳細はコードを参照して下さい。

下記で動かせます。動かし方は13/HardwareSimulatorWasmと同じです。

cd 13/HardwareSimulatorWasmBuiltIn

# test all
TEST=1 RUST_MIN_STACK=3000000 cargo test

nvm i v14.15.1
npm --version
# 6.14.8
node --version
# v14.15.1

npm install
npm start

起動すると画面（ブラウザ）を白から黒に塗り替えていきます。

ビルトイン版のイメージ

雰囲気としては、例えばRAM16Kのビルトイン版は下記のような感じです。ビルトイン版にはサフィックスに構造体は BuiltIn 、関数は _built_in をつけています。

#[derive(Debug, Copy, Clone)]
pub struct RAM16KBuiltIn {
    ram: [word; 16384 /* 14bit */],
}

impl RAM16KBuiltIn {
    pub fn new() -> Self {
        RAM16KBuiltIn {
            ram: [u16_to_word(0b0000_0000_0000_0000); 16384],
        }
    }

    pub fn update(&mut self, clk: bit, input: word, load: bit, address: [bit; 14]) {
        if clk && load {
            self.ram[bit14_to_u16(address) as usize] = input;
        }
    }

    pub fn get(&self, clk: bit, address: [bit; 14]) -> word {
        self.ram[bit14_to_u16(address) as usize]
    }
}

オリジナルと比較すると違いがわかると思います。RAM4Kを使わず自前実装している感じですね。

#[derive(Debug, Copy, Clone)]
pub struct RAM16K {
    rams: [RAM4K; 4]
}

impl RAM16K {
    pub fn new() -> Self {
        RAM16K {
            rams: [RAM4K::new(); 4]
        }
    }

    pub fn update(&mut self, clk: bit, input: word, load: bit, address: [bit; 14]) {
        let address_low = [
            address[0], address[1], address[2], address[3],
            address[4], address[5], address[6], address[7],
            address[8], address[9], address[10], address[11]
        ];
        let address_high = [address[12], address[13]];
        let (a, b, c, d) = dmux4way(load, address_high);
        self.rams[0].update(clk, input, a, address_low);
        self.rams[1].update(clk, input, b, address_low);
        self.rams[2].update(clk, input, c, address_low);
        self.rams[3].update(clk, input, d, address_low);
    }

    pub fn get(&self, clk: bit, address: [bit; 14]) -> word {
        let address_low = [
            address[0], address[1], address[2], address[3],
            address[4], address[5], address[6], address[7],
            address[8], address[9], address[10], address[11]
        ];
        let address_high = [address[12], address[13]];
        mux4way16(
            self.rams[0].get(clk, address_low),
            self.rams[1].get(clk, address_low),
            self.rams[2].get(clk, address_low),
            self.rams[3].get(clk, address_low),
            address_high
        )
    }
}

実装を終えて

動作速度は少し改善しましたがまだまだ遅いです。。*7

まとめ

気の迷いから始めたハードウェアシミュレータのRust実装も無事にブラウザで動かすところまでは辿り着けました。なんとかクリスマスイブに間に合って良かったです。心残りも色々あるので改善していきたいなと思います。

やぱり動作速度はなんとかしたい
- 速度改善はちゃんとボトルネックのホットスポットを計測して進めるべきですね。
Rustらしいコードを書きたい
- せっかく動かすところまではできたのでRustぽい実装にリファクタしたいですね。
HDLより仕組みの理解が進んだ（気がする）
- HDLで定義するよりもRustでnand関数から組み上げていく方がプログラマにはコンピュータの仕組みが理解しやすいように感じました。

*1:最近はデータエンジニアに集中していてものづくり系のコードはしばらく書けていないです...プライベートの時間にオモチャのコードを書いて精神を保っています

*2:第2版も出ましたね。早速買いました。パラパラ見た感じでは第1版より読みやすくなってそうです。この記事が書き終わったら読みたいです。

*3:今回の作成内容は完全に趣味です。仕事とは全く関係ないですがRustに入門してみた記録です。未来の自分への備忘録なのでダラダラ長くなっています。言語入門には動くものを作ってみるのが一番早い。

*4:テストしんどいしデバッグ大変だしハードウェア開発のつらさを体験できました

*5:今回は遅すぎて真っ黒になるのに時間がかかりすぎ、処理に時間がかかりすぎてキーの認識もほぼされないので真っ白にもならないと思いますが。。。

*6:このブログでは説明のためにSDL実装からにしてますが、本当のところはこの書籍を読んでWasmでnand2tetris動かせるのでは？と思ってこのブログのネタが始まりました。実装もWasm版から始めたのですが動かすところまで行けずデバッグの困難さから諦めてネイティブ実装のSDL版に切り替えたのちに動かせたのでWasmに戻ってきて再挑戦しました。

*7:本当はどの程度改善したか計測すべきと思いつつ目視で遅さがわかるレベルなのでやってません。本来は一瞬で画面全てが黒くなるはずなので・・・

2024-03-31

コンピュータシステムの理論と実装の12章のオペレーティングシステムを実装しました

コンピュータシステムの理論と実装 nand2tetris オペレーティングシステム

前回の続きです。今回はコンピュータシステムの理論と実装（以下、nand2tetris本）の12章のオペレーティングシステムを実装してみました。

今回のコード
概要
1. Memory（メモリ操作）
2. Array（配列操作）
3. Math（基本的な演算）
4. String（文字列操作）
5. Output（スクリーンへのテキスト出力）
6. Screen（スクリーンへのグラフィック出力）
7. Keyboard（キーボード入力）
8. Sys（プログラム実行関連）
9. All（Pongゲームによる総合テスト）
まとめ

今回のコード

下記、タグv0.0.5になります。

github.com

下記で動かせます。

git clone -b v0.0.5 https://github.com/nihemak/nand2tetris.git
cd nand2tetris
# download nand2tetris environment
./setup.sh
# test all
./test.sh

概要

今回はオペレーティングシステムにあたる部分（Jack OS）のJack言語による実装です。書籍に従ってクラスごとに単独で実装・テスト確認していきました。最後に全てのコードを結合して総合テストとしてPongゲームを動作させての確認しました。

使い方はtest12.shを参照。

全体を通してエラーコードは書籍の表9-1に従っています。

1. Memory（メモリ操作）

ソースコードは12/1_Memory/Memory.jackです。

ここでは下記を実装しました。

function void init()
function int peek(int address)
function void poke(int address, int value)
function int alloc(int size)
function void deAlloc(Array o)

alloc・deAllocについては実装が楽な first-fit アルゴリズムを採用しました。ちなみに今回はdeAllocした領域を freeList の先頭に戻すようにしているのでallocでの空き領域の探索で早い段階で性能に影響が出るかもしれないです*1。あとフラグメンテーション解消のケアは今回してないです。

2. Array（配列操作）

ソースコードは12/2_Array/Array.jackです。

ここでは下記を実装しました。

function Array new(int size)
method void dispose()

Memory.allocとMemory.deAllocのラッパーになってます。

3. Math（基本的な演算）

ソースコードは12/3_Math/Math.jackです。

ここでは下記を実装しました。

function void init()
function int multiply(int x, int y)
function int divide(int x, int y)
function int sqrt(int x)
function int max(int a, int b)
function int min(int a, int b)
function int abs(int x)
function boolean bit(int x, int j)

ほぼほぼ書籍のアルゴリズムに従っています。ポイントは乗算の計算コストが高いためできるだけ加算で行う工夫をしているところです。このあたりはだいぶ可読性が犠牲になっています。

4. String（文字列操作）

ソースコードは12/4_String/String.jackです。

ここでは下記を実装しました。

constructor String new(int maxLength)
method void dispose()
method int length()
method char charAt(int j)
method void setCharAt(int j, char c)
method String appendChar(char c)
method void eraseLastChar()
method int intValue()
method void setInt(int val)
function char newLine()
function char backSpace()
function char doubleQuote()

内部実装では文字のArrayを使用しています。数値と文字列を変換するintValue・setIntは歯応えがありました。

5. Output（スクリーンへのテキスト出力）

ソースコードは12/5_Output/Output.jackです。

ここでは下記を実装しました。

function void init()
function void initMap()
function void create(int index, int a, int b, int c, int d, int e, int f, int g, int h, int i, int j, int k)
function Array getMap(char c)
function void moveCursor(int i, int j)
function void printChar(char c)
function void printString(String s)
function void printInt(int i)
function void println()
function void backSpace()
function void displayChar(char c)

カーソル操作と文字画像出力で実際の描画はScreenクラスを使いました。スクロールは最低限テストプログラムの出力と一致していればOKとしてほぼ実装せず雑な感じです。

6. Screen（スクリーンへのグラフィック出力）

ソースコードは12/6_Screen/Screen.jackです。

ここでは下記を実装しました。

function void init()
function void clearScreen()
function void setColor(boolean b)
function void drawPixel(int x, int y)
function void drawHorizontalLine(int x1, int x4, int y)
function void drawLine(int x1, int y1, int x2, int y2)
function void drawRectangle(int x1, int y1, int x2, int y2)
function void drawCircle(int x, int y, int r)

メモリマップされたScreenの領域を読み書きすることで描画を行いました。

書籍の通り実装したところあまりにも描画が重たかったため最適化としてdrawHorizontalLine（水平線描画）を追加しました。この関数では描画を「x1->x2」「x2->x3」「x3->x4」の３区間に分けて「x2->x3」を1ワード分の16ピクセル単位で描画して描画ループ処理を削減しました*2。そしてclearScreenやdrawRectangleなどの内部で使うようにしました。結果として高速化しましたが、それでも描画はまだまだ重いのでもっと最適化を考えた方が良いと思います。

7. Keyboard（キーボード入力）

ソースコードは12/7_Keyboard/Keyboard.jackです。

ここでは下記を実装しました。

function void init()
function char keyPressed()
function char readChar()
function String readLine(String message)
function int readInt(String message)

メモリマップされたKeyboardの領域を読み書きすることでキー取得を行いました。

8. Sys（プログラム実行関連）

ソースコードは12/8_Sys/Sys.jackです。

ここでは下記を実装しました。

function void init()
function void halt()
function void wait(int duration)
function void error(int errorCode)

initはプログラム開始時に呼ばれるので他のOKコードのinitとエントリポイントのMain.main呼び出しを行いました。

waitはdurationに応じてループ回数を増やす原始的なものでループ回数は実行するシステム環境依存で調整するみたいです。書籍のリファレンス実装が１durationあたり50回ループになっていたので今回はとりあえず合わせました。

9. All（Pongゲームによる総合テスト）

最後にここまで実装してきたJack OSを全て結合して*311章のPongゲームが動くことを確認しました。

test12.sh:L67-L80

cp -r ./nand2tetris/projects/11/Pong 12/9_All/ && \
cp -r 12/1_Memory/Memory.jack 12/9_All/Pong/ && \
cp -r 12/2_Array/Array.jack 12/9_All/Pong/ && \
cp -r 12/3_Math/Math.jack 12/9_All/Pong/ && \
cp -r 12/4_String/String.jack 12/9_All/Pong/ && \
cp -r 12/5_Output/Output.jack 12/9_All/Pong/ && \
cp -r 12/6_Screen/Screen.jack 12/9_All/Pong/ && \
cp -r 12/7_Keyboard/Keyboard.jack 12/9_All/Pong/ && \
cp -r 12/8_Sys/Sys.jack 12/9_All/Pong/ && \

./nand2tetris/tools/JackCompiler.sh 12/9_All/Pong

# ./nand2tetris/tools/VMEmulator.sh
#   12/9_All/Pong/

結果は無事に動きました！（わーい）ただScreenクラスのせいでだいぶスローです。。さらなる最適化が必要そうです。

まとめ

長かったコンピュータシステムの理論と実装の実装も今回でおしまいです*4。せっかくおもちゃでもCPUからコンパイラ、OSまで１通り作ってみるイメージが持てたので次はもう少し本格的なものづくりに挑戦してみたいですね。今時？だとFPGAでRISC-Vとかかな。低レイヤを気ままに楽しもうと思います。

*1:仮にサイズの小さな領域を開放し次のallocで大きな領域を確保を試みた場合は１件目でfirst-fitしない事になる。もしdeAllocで末尾に戻すようにしたら１件目の空き領域はサイズが大きいことが多いので１件目でfirst-fitしやすい。

*2:1ワード単位にできない「x1->x2」と「x3->x4」は今まで通り1ピクセル単位で描画

*3:ここまではそれぞれ単独でテストしていた。VM エミュレータではJackOSの存在しないコードはエミュレータ側のJackOKで動く。

*4:13章は残ってますが発展の章なので一旦終わり

2024-03-16

コンピュータシステムの理論と実装の11章のコンパイラ#2：コード生成を実装しました

コンピュータシステムの理論と実装 nand2tetris コンパイラ C言語

前回の続きです*1。今回はコンピュータシステムの理論と実装（以下、nand2tetris本）の11章のコンパイラ#2：コード生成をC言語で実装してみました。

今回のコード
概要
シンボルテーブル
- SymbolTableモジュール
- CompilationEngineモジュール
コード生成
まとめ

今回のコード

下記、タグv0.0.4になります。

github.com

下記で動かせます。

git clone -b v0.0.4 https://github.com/nihemak/nand2tetris.git
cd nand2tetris
# download nand2tetris environment
./setup.sh
# test all
./test.sh

概要

今回はコンパイラのコード生成部分です。実装は書籍にしたがって２段階で行いました。

シンボルテーブルを実装し10章で実装した構文解析器を拡張し解析結果である.xmlファイルに付加情報を追加
構文解析器を7章と8章で実装したバーチャルマシンで動く.vmファイルを生成するコマンドに改造

シンボルテーブル

ソースコードは11/JackCompiler/です。

ここではシンボルテーブルを作成し識別子（変数）の下記の情報を管理できるようにしました。

情報	概要
名前	識別子の名前（変数名）
型	`int` or `boolean` or `char` or クラス名
属性(スコープ)	`Static` or `Field` or `Argument` or `Var`
属性内でのindex	属性ごとに0からの連番を付与

そして10章で実装した構文解析器の出力XMLのidentifierタグにシンボル情報を追加しました。

下記で使えます。

test11.sh:L3-L39

cp -r ./nand2tetris/projects/10/Square 11/JackCompiler/ && \
mkdir -p 11/JackCompiler/Square/expect && \
mv 11/JackCompiler/Square/*.xml 11/JackCompiler/Square/expect/
patch -p1 -d 11/JackCompiler/Square/expect < 11/JackCompiler/test/Square.patch

# ...(省略)...

cd 11/JackCompiler/

clang --std=c11 -Wall -Wextra -o JackCompiler main.c JackTokenizer.c JackTokenizerPrivate.c SymbolTable.c SymbolTablePrivate.c CompilationEngine.c

./JackCompiler Square
./JackCompiler ExpressionLessSquare
./JackCompiler ArrayTest

cd -

./nand2tetris/tools/TextComparer.sh 11/JackCompiler/Square/expect/Main.xml 11/JackCompiler/Square/Main.xml 
./nand2tetris/tools/TextComparer.sh 11/JackCompiler/Square/expect/Square.xml 11/JackCompiler/Square/Square.xml 
./nand2tetris/tools/TextComparer.sh 11/JackCompiler/Square/expect/SquareGame.xml 11/JackCompiler/Square/SquareGame.xml 
./nand2tetris/tools/TextComparer.sh 11/JackCompiler/ExpressionLessSquare/expect/Main.xml 11/JackCompiler/ExpressionLessSquare/Main.xml
./nand2tetris/tools/TextComparer.sh 11/JackCompiler/ExpressionLessSquare/expect/Square.xml 11/JackCompiler/ExpressionLessSquare/Square.xml
./nand2tetris/tools/TextComparer.sh 11/JackCompiler/ExpressionLessSquare/expect/SquareGame.xml 11/JackCompiler/ExpressionLessSquare/SquareGame.xml
./nand2tetris/tools/TextComparer.sh 11/JackCompiler/ArrayTest/expect/Main.xml 11/JackCompiler/ArrayTest/Main.xml

SymbolTableモジュール

シンボルテーブルを管理するためのモジュールです。

CompilationEngineモジュールで利用する関数はSymbolTable.hで下記のように定義しました。symbol_table構造体はtypedefして定義はSymbolTable.c内に隠蔽するようにしてオブジェクトとして使うようにしました。それぞれの実装はSymbolTable.cで行いました。

11/JackCompiler/SymbolTable.h:L4-L21

typedef enum {
    SYMBOL_TABLE_KIND_STATIC = 1,
    SYMBOL_TABLE_KIND_FIELD,
    SYMBOL_TABLE_KIND_ARG,
    SYMBOL_TABLE_KIND_VAR,
    SYMBOL_TABLE_KIND_NONE,
} SymbolTable_Kind;

typedef struct symbol_table * SymbolTable;

SymbolTable SymbolTable_init();
void SymbolTable_startSubroutine(SymbolTable thisObject);
void SymbolTable_define(SymbolTable thisObject, char *name, char *type, SymbolTable_Kind kind);
int SymbolTable_varCount(SymbolTable thisObject, SymbolTable_Kind kind);
SymbolTable_Kind SymbolTable_kindOf(SymbolTable thisObject, char *name);
void SymbolTable_typeOf(SymbolTable thisObject, char *name, char *type);
int SymbolTable_indexOf(SymbolTable thisObject, char *name);
void SymbolTable_delete(SymbolTable thisObject);

またSymbolTable.c内で使う関数はSymbolTablePrivate.hで下記のように定義しSymbolTablePrivate.cで実装しました。

11/JackCompiler/SymbolTablePrivate.h:L8-L23

#define HASH_TABLE_BUCKET_NUM 50

typedef struct hash_table_bucket
{
    char key[JACK_TOKEN_SIZE];
    char type[JACK_TOKEN_SIZE];
    SymbolTable_Kind kind;
    int index;

    struct hash_table_bucket *next;
} HashTableBucket;

void HashTable_init(HashTableBucket *hash_table[]);
bool HashTable_find(HashTableBucket *hash_table[], char *key, HashTableBucket **pp_ret);
void HashTable_set(HashTableBucket *hash_table[], char* key, char *type, SymbolTable_Kind kind, int index);
void HashTable_deleteAll(HashTableBucket *hash_table[]);

シンボルの管理のためにはハッシュテーブルを実装しました。実装にあたっては定本　Ｃプログラマのためのアルゴリズムとデータ構造の 8. ハッシュ法 の 8.3. チェイン法 を参考にしました*2。効率は全く重視していないのでハッシュ関数は適当です。

11/JackCompiler/SymbolTablePrivate.c:L5-L60

int hash(char *s)
{
    int i = 0;
    while (*s) {
        i += *s++;
    }
    return i % HASH_TABLE_BUCKET_NUM;
}

void HashTable_init(HashTableBucket *hash_table[])
{
    for (int i = 0; i < HASH_TABLE_BUCKET_NUM; i++) {
        hash_table[i] = NULL;
    }
}

bool HashTable_find(HashTableBucket *hash_table[], char *key, HashTableBucket **pp_ret)
{
    for (HashTableBucket *p = hash_table[hash(key)]; p != NULL; p = p->next) {
        if (strcmp(key, p->key) == 0) {
            *pp_ret = p;
            return true;
        }
    }
    return false;
}

void HashTable_set(HashTableBucket *hash_table[], char* key, char *type, SymbolTable_Kind kind, int index)
{
    HashTableBucket *p;
    if (! HashTable_find(hash_table, key, &p)) {
        p = (HashTableBucket *)malloc(sizeof(HashTableBucket));
    }

    strcpy(p->key, key);
    strcpy(p->type, type);
    p->kind = kind;
    p->index = index;

    int h = hash(key);
    p->next = hash_table[h];
    hash_table[h] = p;
}

void HashTable_deleteAll(HashTableBucket *hash_table[])
{
    for (int i = 0; i < HASH_TABLE_BUCKET_NUM; i++) {
        HashTableBucket *current = hash_table[i];
        while (current != NULL) {
            HashTableBucket *next = current->next;
            free(current);
            current = next;
        }
        hash_table[i] = NULL;
    }
}

シンボルテーブルは変数の生存期間に応じてクラススコープ用とサブルーチンスコープ用の２つのハッシュテーブルを用意する事で実現しました。

11/JackCompiler/SymbolTable.c:L7-L17

typedef struct symbol_table * SymbolTable;
struct symbol_table
{
    HashTableBucket *class_hash_table[HASH_TABLE_BUCKET_NUM];
    int static_count;
    int field_count;

    HashTableBucket *subroutine_hash_table[HASH_TABLE_BUCKET_NUM];
    int arg_count;
    int var_count;
};

それぞれ実装の詳細はソースコードを参照。

CompilationEngineモジュール

10章で作成した.jackファイルを構文解析して.xmlファイルに出力するためのモジュールです。 SymbolTableモジュールを使って識別子にシンボル情報を付加して.xmlファイル出力するように改造しました。

SymbolTableモジュールを用いた処理を下記に追加しました。

場所	SymbolTableモジュールを用いた処理
`CompilationEngine_init`	`SymbolTable_init` によるシンボルテーブルの初期化
`CompilationEngine_compileClass`	終了タイミングで `SymbolTable_delete` と `SymbolTable_init` によるシンボルテーブルの初期化
`CompilationEngine_compileClassVarDec`	変数宣言タイミングで `SymbolTable_define` によるシンボルテーブルの記録
`CompilationEngine_compileSubroutine`	`SymbolTable_startSubroutine` によるシンボルテーブル・サブルーチンの初期化
`CompilationEngine_compileParameterList`	変数宣言タイミングで `SymbolTable_define` によるシンボルテーブルの記録
`CompilationEngine_compileVarDec`	変数宣言タイミングで `SymbolTable_define` によるシンボルテーブルの記録

またidentifierタグの出力関数の引数にシンボル情報を追加してidentifierタグにシンボル情報を含めるようにしました。

11/JackCompiler/CompilationEngine.c:L683-L725

void writeIdentifier(FILE *fp, JackTokenizer tokenizer, char *category, char *status, SymbolTable symbolTable)
{
    char token[JACK_TOKEN_SIZE];
    JackTokenizer_identifier(tokenizer, token);
    writeIdentifierByToken(fp, token, category, status, symbolTable);
}

// ...(省略)...

void writeIdentifierByToken(FILE *fp, char *token, char *category, char *status, SymbolTable symbolTable)
{
    fprintf(fp, "<identifier category=\"%s\" status=\"%s\"", category, status);
    if (symbolTable != NULL) {
        char kindStr[JACK_TOKEN_SIZE];
        getIdentifierKindString(symbolTable, token, kindStr);

        char typeStr[JACK_TOKEN_SIZE];
        SymbolTable_typeOf(symbolTable, token, typeStr);
        fprintf(fp, " kind=\"%s\" type=\"%s\" index=\"%d\"", kindStr, typeStr, SymbolTable_indexOf(symbolTable, token));
    }
    fprintf(fp, "> %s </identifier>\n", token);
}

テストの正解データについては提供されていないため目視でチェックした結果データを元にpatchを作成し自動テストに組み込みました。

11/JackCompiler/test

ArrayTest.patch
ExpressionLessSquare.patch
Square.patch

test11.sh:L6

patch -p1 -d 11/JackCompiler/Square/expect < 11/JackCompiler/test/Square.patch

patchの作成は下記で行いました。（xmlのインデントが異なるため-wで空白を無視しています）

diff -u -w -r expect expect_fix > ArrayTest.patch

コード生成

ここではバーチャルマシンへの標準マッピング仕様に基づき各構文をコードに変換し.vmファイルへ出力するようにしていきました。段階的に対応構文を増やしていくテストプログラムが用意されているのでそれにしたがって実装を進めていきました。

最小限の構文要素

ソースコードは11/JackCompiler2/です。

ここでは下記を行いました。

コンパイラの出力を構文解析結果.xmlファイルからバーチャルマシンコード.vmファイルに変更
最小限の構文要素に対応（定数値の算術式、do文、return文）
テストコードの Seven がコンパイルでき動作確認できるところを目指す

下記で使えます。

test11.sh:L41-L53

cp -r ./nand2tetris/projects/11/Seven 11/JackCompiler2/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler2/Seven/

cd 11/JackCompiler2/

clang --std=c11 -Wall -Wextra -o JackCompiler main.c JackTokenizer.c JackTokenizerPrivate.c SymbolTable.c SymbolTablePrivate.c VMWriter.c CompilationEngine.c

./JackCompiler Seven

cd -

# ./nand2tetris/tools/VMEmulator.sh
#   11/JackCompiler2/Seven

動かすためにOS提供関数の./nand2tetris/tools/OS/以下のファイルを使っています。
テストは自動実行できないので手動で確認する必要があります*3。

実行するとScreenエリアに 7 と表示されます。

main.c (JackCompilerモジュール)

コンパイラの出力を構文解析結果.xmlファイルからバーチャルマシンコード.vmファイルに変更しました。

差分は下記の通りです。

$ diff 11/JackCompiler/main.c 11/JackCompiler2/main.c 
8c8
< #define XML_FILENAME_MAX_LENGTH (JACK_FILENAME_MAX_LENGTH - 1)  // length('.jack') - length('.xml') = 1
---
> #define VM_FILENAME_MAX_LENGTH (JACK_FILENAME_MAX_LENGTH - 2)  // length('.jack') - length('.vm') = 2
11,13c11,13
< int analyzeByJackDir(DIR *dpJack, char *jackDirName);
< int analyzeByJackFile(char *jackFileName);
< int analyze(char *xmlFilePath, char *jackFilePath);
---
> int compileByJackDir(DIR *dpJack, char *jackDirName);
> int compileByJackFile(char *jackFileName);
> int compile(char *vmFilePath, char *jackFilePath);
16,17c16,17
< void createXmlFilePathFromDirName(char *jackDirName, char *jackFileName, char *xmlFilePath);
< void createXmlFilePathFromJackFileName(char *jackFileName, char *xmlFilePath);
---
> void createVmFilePathFromDirName(char *jackDirName, char *jackFileName, char *vmFilePath);
> void createVmFilePathFromJackFileName(char *jackFileName, char *vmFilePath);
37c37
<         int exitNo = analyzeByJackDir(dpJack, jackFileOrDirName);
---
>         int exitNo = compileByJackDir(dpJack, jackFileOrDirName);
41c41
<         return analyzeByJackFile(jackFileOrDirName);
---
>         return compileByJackFile(jackFileOrDirName);
50c50
< int analyzeByJackDir(DIR *dpJack, char *jackDirName)
---
> int compileByJackDir(DIR *dpJack, char *jackDirName)
53c53
<     char xmlFilePath[JACK_DIRNAME_MAX_LENGTH + XML_FILENAME_MAX_LENGTH + 1];
---
>     char vmFilePath[JACK_DIRNAME_MAX_LENGTH + VM_FILENAME_MAX_LENGTH + 1];
88,89c88,89
<         createXmlFilePathFromDirName(jackDirName, jackFileName, xmlFilePath);
<         if (analyze(xmlFilePath, jackFilePath) != 0) {
---
>         createVmFilePathFromDirName(jackDirName, jackFileName, vmFilePath);
>         if (compile(vmFilePath, jackFilePath) != 0) {
97c97
< int analyzeByJackFile(char *jackFileName)
---
> int compileByJackFile(char *jackFileName)
99c99
<     char xmlFilePath[XML_FILENAME_MAX_LENGTH];
---
>     char vmFilePath[VM_FILENAME_MAX_LENGTH];
117,118c117,118
<     createXmlFilePathFromJackFileName(jackFileName, xmlFilePath);
<     return analyze(xmlFilePath, jackFileName);
---
>     createVmFilePathFromJackFileName(jackFileName, vmFilePath);
>     return compile(vmFilePath, jackFileName);
121c121
< int analyze(char *xmlFilePath, char *jackFilePath)
---
> int compile(char *vmFilePath, char *jackFilePath)
123c123
<     FILE *fpJack, *fpXml;
---
>     FILE *fpJack, *fpVm;
131,132c131,132
<     if ((fpXml = fopen(xmlFilePath, "w")) == NULL) {
<         fprintf(stderr, "Error: xml file not open (%s)\n", xmlFilePath);
---
>     if ((fpVm = fopen(vmFilePath, "w")) == NULL) {
>         fprintf(stderr, "Error: vm file not open (%s)\n", vmFilePath);
137c137
<     compilationEngine = CompilationEngine_init(fpJack, fpXml);
---
>     compilationEngine = CompilationEngine_init(fpJack, fpVm);
140c140
<     fclose(fpXml);
---
>     fclose(fpVm);
172c172
< void createXmlFilePathFromDirName(char *jackDirName, char *jackFileName, char *xmlFilePath)
---
> void createVmFilePathFromDirName(char *jackDirName, char *jackFileName, char *vmFilePath)
174,178c174,178
<     // xmlFilePath is {jackDirName}/{jackFileName} - ".jack" + ".xml"
<     strcpy(xmlFilePath, jackDirName);
<     strcat(xmlFilePath, "/");
<     strncat(xmlFilePath, jackFileName, strlen(jackFileName) - strlen(".jack"));
<     strcat(xmlFilePath, ".xml");
---
>     // vmFilePath is {jackDirName}/{jackFileName} - ".jack" + ".vm"
>     strcpy(vmFilePath, jackDirName);
>     strcat(vmFilePath, "/");
>     strncat(vmFilePath, jackFileName, strlen(jackFileName) - strlen(".jack"));
>     strcat(vmFilePath, ".vm");
181c181
< void createXmlFilePathFromJackFileName(char *jackFileName, char *xmlFilePath)
---
> void createVmFilePathFromJackFileName(char *jackFileName, char *vmFilePath)
183,184c183,184
<     // XmlFilePath is {jackFileName} - ".jack" + ".xml"
<     size_t xmlFileNamePrefixLength = strlen(jackFileName) - strlen(".jack");
---
>     // VmFilePath is {jackFileName} - ".jack" + ".vm"
>     size_t vmFileNamePrefixLength = strlen(jackFileName) - strlen(".jack");
186,188c186,188
<     strncpy(xmlFilePath, jackFileName, xmlFileNamePrefixLength);
<     xmlFilePath[xmlFileNamePrefixLength] = '\0';
<     strcat(xmlFilePath, ".xml");
---
>     strncpy(vmFilePath, jackFileName, vmFileNamePrefixLength);
>     vmFilePath[vmFileNamePrefixLength] = '\0';
>     strcat(vmFilePath, ".vm");

VMWriterモジュール

VMコマンドの構文に従いVMコマンドをファイルに書き出すモジュールです。

CompilationEngineモジュールで利用する関数はVMWriter.hで下記のように定義しました。vm_writer構造体はtypedefして定義はVMWriter.c内に隠蔽するようにしてオブジェクトとして使うようにしました。それぞれの実装はVMWriter.cで行いました。

11/JackCompiler2/VMWriter.h:L4-L21

typedef enum {
    VM_WRITER_SEGMENT_CONST = 1,
    VM_WRITER_SEGMENT_ARG,
    VM_WRITER_SEGMENT_LOCAL,
    VM_WRITER_SEGMENT_STATIC,
    VM_WRITER_SEGMENT_THIS,
    VM_WRITER_SEGMENT_THAT,
    VM_WRITER_SEGMENT_POINTER,
    VM_WRITER_SEGMENT_TEMP,
} VMWriter_Segment;

typedef enum {
    VM_WRITER_COMMAND_ADD = 1,
    VM_WRITER_COMMAND_SUB,
    VM_WRITER_COMMAND_NEG,
    VM_WRITER_COMMAND_EQ,
    VM_WRITER_COMMAND_GT,
    VM_WRITER_COMMAND_LT,
    VM_WRITER_COMMAND_AND,
    VM_WRITER_COMMAND_OR,
    VM_WRITER_COMMAND_NOT,
} VMWriter_Command;

typedef struct vm_writer * WMWriter;

WMWriter WMWriter_init(FILE *fpVm);
void VMWriter_writePush(WMWriter thisObject, VMWriter_Segment segment, int index);
void VMWriter_writePop(WMWriter thisObject, VMWriter_Segment segment, int index);
void VMWriter_writeArithmetic(WMWriter thisObject, VMWriter_Command command);
void VMWriter_writeLabel(WMWriter thisObject, char *label);
void VMWriter_writeGoto(WMWriter thisObject, char *label);
void VMWriter_writeIf(WMWriter thisObject, char *label);
void VMWriter_writeCall(WMWriter thisObject, char *name, int nArgs);
void VMWriter_writeFunction(WMWriter thisObject, char *name, int nLocals);
void VMWriter_writeReturn(WMWriter thisObject);
void VMWriter_close(WMWriter thisObject);

実装はfprintfでファイルに書き出しているだけです。

11/JackCompiler2/VMWriter.c

CompilationEngineモジュール

以降の対応のためにXML出力向けに共通化していた部分をVM出力しやすくリファクタリングしました。

11/JackCompiler2/CompilationEngine.c

CompilationEngine_compileSubroutine

サブルーチンはローカル変数の数を 0 で決め打ちしてテストを動かすための最小限の実装にしました。

11/JackCompiler2/CompilationEngine.c:L118-L179

void CompilationEngine_compileSubroutine(CompilationEngine thisObject)
{
    // ...(省略)...

    char functionName[JACK_TOKEN_SIZE];
    sprintf(functionName, "%s.%s", thisObject->className, subroutineName);
    VMWriter_writeFunction(thisObject->vmWriter, functionName, 0 /* FIXME */);

    // ...(省略)...
}

CompilationEngine_compileDo

サブルーチン名は クラス名.メソッド名 の形式のみ対応しました。
do文は戻り値を使わないのでtempセグメントに捨てるようにしました。

11/JackCompiler2/CompilationEngine.c:L284-L342

void CompilationEngine_compileDo(CompilationEngine thisObject)
{
    // ...(省略)...

    // subroutineName | (className | varName)
    char token[JACK_TOKEN_SIZE];
    JackTokenizer_identifier(thisObject->tokenizer, token);
    JackTokenizer_advance(thisObject->tokenizer);

    sprintf(functionName, "%s", token);

    // '(' or '.'
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    if (isSymbolToken(thisObject, ".")) {
        // (className | varName) used
        // ...(省略)...

        // subroutineName (subroutine used)
        JackTokenizer_identifier(thisObject->tokenizer, identifier);
        JackTokenizer_advance(thisObject->tokenizer);

        sprintf(functionName, "%s%s%s", functionName, symbol, identifier);

        // '('
        JackTokenizer_symbol(thisObject->tokenizer, symbol);
    } else {
        // token is subroutineName (subroutine used)
    }
    JackTokenizer_advance(thisObject->tokenizer);

    int nArgs = CompilationEngine_compileExpressionList(thisObject);

    // ...(省略)...

    VMWriter_writeCall(thisObject->vmWriter, functionName, nArgs);
    VMWriter_writePop(thisObject->vmWriter, VM_WRITER_SEGMENT_TEMP, 0);
}

CompilationEngine_compileReturn

return文はvoidのみ対応として戻り値を 0 固定にしました。

11/JackCompiler2/CompilationEngine.c:L416-L436

void CompilationEngine_compileReturn(CompilationEngine thisObject)
{
    // ...(省略)...

    VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_CONST, 0);  /* FIXME */
    VMWriter_writeReturn(thisObject->vmWriter);
}

CompilationEngine_compileExpression

加算と乗算のみ対応しました。乗算はOSが提供するMath.multiplyを呼び出すようにしました。
演算が逆ポーランドの順番になるようにしました。

11/JackCompiler2/CompilationEngine.c:L488-L510

void CompilationEngine_compileExpression(CompilationEngine thisObject)
{
    char symbol[JACK_TOKEN_SIZE];

    CompilationEngine_compileTerm(thisObject);

    while (inSymbolListToken(thisObject, "+", "-", "*",  "/", "&", "|", "<", ">", "=", NULL)) {
        // op
        JackTokenizer_symbol(thisObject->tokenizer, symbol);
        JackTokenizer_advance(thisObject->tokenizer);

        CompilationEngine_compileTerm(thisObject);

        // op is after terms because it is Reverse Polish Notation (RPN)
        // term1 term2 op (ex. 1+(2*3) => 1(2*3)+ => 1(23*)+)
        if (strcmp(symbol, "+") == 0) {
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_ADD);
        }
        if (strcmp(symbol, "*") == 0) {
            VMWriter_writeCall(thisObject->vmWriter, "Math.multiply", 2);
        }
    }
}

CompilationEngine_compileTerm

数値のみ対応しました。

11/JackCompiler2/CompilationEngine.c:L515-L607

void CompilationEngine_compileTerm(CompilationEngine thisObject)
{
    // ...(省略)...

    if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_INT_CONST) {
        // integerConstant
        JackTokenizer_intVal(thisObject->tokenizer, &intVal);
        JackTokenizer_advance(thisObject->tokenizer);

        VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_CONST, intVal);
    } else if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_STRING_CONST) {
        // ...(省略)...
    } else {    // varName | varName '[' expression ']' | subroutineCall
        // ...(省略)...
    }
}

全ての手続き的要素

ソースコードは11/JackCompiler3/です。

ここでは下記を行いました。

全ての手続き的要素に対応（配列とメソッド呼び出しを除く式、ファンクション、文）
テストコードの ConvertToBin がコンパイルでき動作確認できるところを目指す

下記で使えます。

test11.sh:L55-L72

cp -r ./nand2tetris/projects/11/Seven 11/JackCompiler3/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler3/Seven/

cp -r ./nand2tetris/projects/11/ConvertToBin 11/JackCompiler3/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler3/ConvertToBin/

cd 11/JackCompiler3/

clang --std=c11 -Wall -Wextra -o JackCompiler main.c JackTokenizer.c JackTokenizerPrivate.c SymbolTable.c SymbolTablePrivate.c VMWriter.c CompilationEngine.c

./JackCompiler Seven
./JackCompiler ConvertToBin

cd -

# ./nand2tetris/tools/VMEmulator.sh
#   11/JackCompiler3/Seven
#   11/JackCompiler3/ConvertToBin

動かすためにOS提供関数の./nand2tetris/tools/OS/以下のファイルを使っています。
テストは自動実行できないので手動で確認する必要があります*4。

RAM8000番地に数値を設定して実行すると2進数に変換され8001番地以降に設定されます。 (今回は221をセットしたので0xDD = 0000000011011101がセットされた)

CompilationEngineモジュール

CompilationEngine_compileSubroutine

サブルーチンのローカル変数の数に対応しました。

11/JackCompiler3/CompilationEngine.c:L122-L188

void CompilationEngine_compileSubroutine(CompilationEngine thisObject)
{
    // ...(省略)...

    // subroutineBody
    {
        // ...(省略)...

        VMWriter_writeFunction(
            thisObject->vmWriter,
            functionName,
            SymbolTable_varCount(thisObject->symbolTable, SYMBOL_TABLE_KIND_VAR)
        );

        // ...(省略)...
    }
}

CompilationEngine_compileLet

変数への代入に対応しました。

11/JackCompiler3/CompilationEngine.c:L354-L396

void CompilationEngine_compileLet(CompilationEngine thisObject)
{
    // ...(省略)...

    VMWriter_writePop(
        thisObject->vmWriter,
        kind == SYMBOL_TABLE_KIND_VAR ? VM_WRITER_SEGMENT_LOCAL : VM_WRITER_SEGMENT_ARG,
        SymbolTable_indexOf(thisObject->symbolTable, varName)
    );

    // ...(省略)...
}

CompilationEngine_compileWhile

while文に対応しました。

11/JackCompiler3/CompilationEngine.c:L399-L441

void CompilationEngine_compileWhile(CompilationEngine thisObject)
{
    JackTokenizer_Keyword keyword;
    char symbol[JACK_TOKEN_SIZE];

    // 'while'
    keyword = JackTokenizer_keyword(thisObject->tokenizer);
    JackTokenizer_advance(thisObject->tokenizer);

    char labelExp[JACK_TOKEN_SIZE], labelEnd[JACK_TOKEN_SIZE];
    sprintf(labelExp, "%s$$$WHILE_EXP.%d", thisObject->className, thisObject->whileLabelCount);
    sprintf(labelEnd, "%s$$$WHILE_END.%d", thisObject->className, thisObject->whileLabelCount);
    thisObject->whileLabelCount++;

    VMWriter_writeLabel(thisObject->vmWriter, labelExp);

    // '('
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    JackTokenizer_advance(thisObject->tokenizer);

    CompilationEngine_compileExpression(thisObject);

    // ')'
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    JackTokenizer_advance(thisObject->tokenizer);

    VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_NOT);
    VMWriter_writeIf(thisObject->vmWriter, labelEnd);

    // '{'
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    JackTokenizer_advance(thisObject->tokenizer);

    CompilationEngine_compileStatements(thisObject);

    VMWriter_writeGoto(thisObject->vmWriter, labelExp);

    // '}'
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    JackTokenizer_advance(thisObject->tokenizer);

    VMWriter_writeLabel(thisObject->vmWriter, labelEnd);
}

CompilationEngine_compileReturn

値のreturnがない場合のみ 0 を戻り値にするようにしました。

11/JackCompiler3/CompilationEngine.c:L444-L465

void CompilationEngine_compileReturn(CompilationEngine thisObject)
{
    // ...(省略)...

    // expression or ';'
    if (! isSymbolToken(thisObject, ";")) {
        CompilationEngine_compileExpression(thisObject);
    } else {
        VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_CONST, 0);
    }

    // ...(省略)...

    VMWriter_writeReturn(thisObject->vmWriter);
}

CompilationEngine_compileIf

if文に対応しました。

11/JackCompiler3/CompilationEngine.c:L468-L528

void CompilationEngine_compileIf(CompilationEngine thisObject)
{
    // ...(省略)...

    char labelTrue[JACK_TOKEN_SIZE], labelFalse[JACK_TOKEN_SIZE], labelEnd[JACK_TOKEN_SIZE];
    sprintf(labelTrue, "%s$$$IF_TRUE.%d", thisObject->className, thisObject->ifLabelCount);
    sprintf(labelFalse, "%s$$$IF_FALSE.%d", thisObject->className, thisObject->ifLabelCount);
    sprintf(labelEnd, "%s$$$IF_END.%d", thisObject->className, thisObject->ifLabelCount);
    thisObject->ifLabelCount++;

    // '('
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    JackTokenizer_advance(thisObject->tokenizer);

    CompilationEngine_compileExpression(thisObject);

    // ')'
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    JackTokenizer_advance(thisObject->tokenizer);

    VMWriter_writeIf(thisObject->vmWriter, labelTrue);
    VMWriter_writeGoto(thisObject->vmWriter, labelFalse);
    VMWriter_writeLabel(thisObject->vmWriter, labelTrue);

    // '{'
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    JackTokenizer_advance(thisObject->tokenizer);

    CompilationEngine_compileStatements(thisObject);

    // '}'
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    JackTokenizer_advance(thisObject->tokenizer);

    VMWriter_writeGoto(thisObject->vmWriter, labelEnd);
    VMWriter_writeLabel(thisObject->vmWriter, labelFalse);

    // 'else' or not
    if (isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_ELSE)) {
        // ...(省略)...
    }

    VMWriter_writeLabel(thisObject->vmWriter, labelEnd);
}

CompilationEngine_compileExpression

全ての演算子に対応しました。

11/JackCompiler3/CompilationEngine.c:L532-L575

void CompilationEngine_compileExpression(CompilationEngine thisObject)
{
    // ...(省略)...
        if (strcmp(symbol, "+") == 0) {
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_ADD);
        }
        if (strcmp(symbol, "-") == 0) {
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_SUB);
        }
        if (strcmp(symbol, "*") == 0) {
            VMWriter_writeCall(thisObject->vmWriter, "Math.multiply", 2);
        }
        if (strcmp(symbol, "/") == 0) {
            VMWriter_writeCall(thisObject->vmWriter, "Math.divide", 2);
        }
        if (strcmp(symbol, "&") == 0) {
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_AND);
        }
        if (strcmp(symbol, "|") == 0) {
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_OR);
        }
        if (strcmp(symbol, "<") == 0) {
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_LT);
        }
        if (strcmp(symbol, ">") == 0) {
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_GT);
        }
        if (strcmp(symbol, "=") == 0) {
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_EQ);
        }
    // ...(省略)...
}

CompilationEngine_compileTerm

TRUE, FALSE, NULLに対応しました
単項演算の -, ~に対応しました
サブルーチン呼び出しに対応しました
変数参照（ローカル変数、パラメータ変数）に対応しました

11/JackCompiler3/CompilationEngine.c:L580-L694

void CompilationEngine_compileTerm(CompilationEngine thisObject)
{
    // ...(省略)...

    if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_INT_CONST) {
        // ...(省略)...
    } else if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_STRING_CONST) {
        // ...(省略)...
    } else if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_KEYWORD) {
         // ...(省略)...

        if (keyword == JACK_TOKENIZER_KEYWORD_TRUE) {
            VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_CONST, 0);
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_NOT);
        }
        if (keyword == JACK_TOKENIZER_KEYWORD_FALSE || keyword == JACK_TOKENIZER_KEYWORD_NULL) {
            VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_CONST, 0);
        }
    } else if (isSymbolToken(thisObject, "(")) {    // '(' expression ')'
        // ...(省略)...
    } else if (inSymbolListToken(thisObject, "-", "~", NULL)) { // unaryOp term
        // ...(省略)...

        VMWriter_writeArithmetic(
            thisObject->vmWriter,
            strcmp(symbol, "-") == 0 ? VM_WRITER_COMMAND_NEG : VM_WRITER_COMMAND_NOT
        );
    } else {    // varName | varName '[' expression ']' | subroutineCall
        // varName | subroutineName | className (used)
        char token[JACK_TOKEN_SIZE];
        JackTokenizer_identifier(thisObject->tokenizer, token);
        SymbolTable_Kind kind = SymbolTable_kindOf(thisObject->symbolTable, token);
        if (kind == SYMBOL_TABLE_KIND_NONE) {
            // token is className
        }
        JackTokenizer_advance(thisObject->tokenizer);

        // '[' or '(' or '.' or not
        if (isSymbolToken(thisObject, "[")) {
            // token is Array of varName (varName[])

            JackTokenizer_symbol(thisObject->tokenizer, symbol);
            JackTokenizer_advance(thisObject->tokenizer);

            CompilationEngine_compileExpression(thisObject);

            // ']'
            JackTokenizer_symbol(thisObject->tokenizer, symbol);
            JackTokenizer_advance(thisObject->tokenizer);
        } else if (inSymbolListToken(thisObject, "(", ".", NULL)) {
            char functionName[JACK_TOKEN_SIZE];
            sprintf(functionName, "%s", token);
            if (isSymbolToken(thisObject, "(")) {
                // token is subroutineName (subroutine used)
            } else {    // "."
                // token is (className | varName)
            }

            // '(' or '.'
            JackTokenizer_symbol(thisObject->tokenizer, symbol);
            if (isSymbolToken(thisObject, ".")) {
                JackTokenizer_advance(thisObject->tokenizer);

                // subroutineName (subroutine used)
                JackTokenizer_identifier(thisObject->tokenizer, identifier);
                JackTokenizer_advance(thisObject->tokenizer);

                sprintf(functionName, "%s%s%s", functionName, symbol, identifier);

                // '('
                JackTokenizer_symbol(thisObject->tokenizer, symbol);
            }
            JackTokenizer_advance(thisObject->tokenizer);

            int nArgs = CompilationEngine_compileExpressionList(thisObject);

            // ')'
            JackTokenizer_symbol(thisObject->tokenizer, symbol);
            JackTokenizer_advance(thisObject->tokenizer);

            VMWriter_writeCall(thisObject->vmWriter, functionName, nArgs);
        } else {
            // token is varName
            VMWriter_writePush(
                thisObject->vmWriter,
                kind == SYMBOL_TABLE_KIND_VAR ? VM_WRITER_SEGMENT_LOCAL : VM_WRITER_SEGMENT_ARG,
                SymbolTable_indexOf(thisObject->symbolTable, token)
            );
        }
    }
}

オブジェクト指向の構成要素

ソースコードは11/JackCompiler4/です。

ここでは下記を行いました。

オブジェクト指向の構成要素に対応（コンストラクタ、メソッド、フィールド、メソッド呼び出しを含む式）
テストコードの Square がコンパイルでき動作確認できるところを目指す

下記で使えます。

test11.sh:L74-L96

cp -r ./nand2tetris/projects/11/Seven 11/JackCompiler4/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler4/Seven/

cp -r ./nand2tetris/projects/11/ConvertToBin 11/JackCompiler4/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler4/ConvertToBin/

cp -r ./nand2tetris/projects/11/Square 11/JackCompiler4/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler4/Square/

cd 11/JackCompiler4/

clang --std=c11 -Wall -Wextra -o JackCompiler main.c JackTokenizer.c JackTokenizerPrivate.c SymbolTable.c SymbolTablePrivate.c VMWriter.c CompilationEngine.c

./JackCompiler Seven
./JackCompiler ConvertToBin
./JackCompiler Square

cd -

# ./nand2tetris/tools/VMEmulator.sh
#   11/JackCompiler4/Seven
#   11/JackCompiler4/ConvertToBin
#   11/JackCompiler4/Square

動かすためにOS提供関数の./nand2tetris/tools/OS/以下のファイルを使っています。
テストは自動実行できないので手動で確認する必要があります*5。

実行するとScreenエリアに黒い四角が表示されて上下左右に動かすことや大きさを変えることができます。

CompilationEngineモジュール

CompilationEngine_compileSubroutine

コンストラクタの場合は Memory.allocでフィールド領域を確保しpointerセグメントの0番目(this)にセットしました
メソッドの場合は第一引数に自身のオブジェクトが指定されている前提にしました

11/JackCompiler4/CompilationEngine.c:L121-L203

void CompilationEngine_compileSubroutine(CompilationEngine thisObject)
{
    // ...(省略)...

    CompilationEngine_compileParameterList(thisObject);

    if (functionKind == JACK_TOKENIZER_KEYWORD_METHOD) {
        // b.mult(5) => mult(b,5)
        // it is ok because "this" is keyword, not verName
        SymbolTable_define(thisObject->symbolTable, "this", thisObject->className, SYMBOL_TABLE_KIND_ARG);
    }

    // ...(省略)...

    // subroutineBody
    {
        // '{'
        JackTokenizer_symbol(thisObject->tokenizer, symbol);
        JackTokenizer_advance(thisObject->tokenizer);

        // 'var' or statements or '}'
        while (isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_VAR)) {
            CompilationEngine_compileVarDec(thisObject);
        }
        VMWriter_writeFunction(
            thisObject->vmWriter,
            functionName,
            SymbolTable_varCount(thisObject->symbolTable, SYMBOL_TABLE_KIND_VAR)
        );
        if (functionKind == JACK_TOKENIZER_KEYWORD_CONSTRUCTION) {
            int fieldCount = SymbolTable_varCount(thisObject->symbolTable, SYMBOL_TABLE_KIND_FIELD);
            VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_CONST, fieldCount);
            VMWriter_writeCall(thisObject->vmWriter, "Memory.alloc", 1);
            VMWriter_writePop(thisObject->vmWriter, VM_WRITER_SEGMENT_POINTER, 0);
        }
        if (functionKind == JACK_TOKENIZER_KEYWORD_METHOD) {
            VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_ARG, 0);
            VMWriter_writePop(thisObject->vmWriter, VM_WRITER_SEGMENT_POINTER, 0);
        }

        // statements or '}'
        if (! isSymbolToken(thisObject, "}")) {
            CompilationEngine_compileStatements(thisObject);
        }

        // '}'
        JackTokenizer_symbol(thisObject->tokenizer, symbol);
        JackTokenizer_advance(thisObject->tokenizer);
    }
}

CompilationEngine_compileDo

フィールド変数経由でのサブルーチン呼び出しに対応しました
メソッド呼び出しの場合は第１引数にオブジェクトを指定するようにしました

11/JackCompiler4/CompilationEngine.c:L308-L391

void CompilationEngine_compileDo(CompilationEngine thisObject)
{
    // ...(省略)...

    // '(' or '.'
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    if (isSymbolToken(thisObject, ".")) {
        // (className | varName) used
        SymbolTable_Kind functionKind = SymbolTable_kindOf(thisObject->symbolTable, token);
        JackTokenizer_advance(thisObject->tokenizer);

        // subroutineName (subroutine used)
        JackTokenizer_identifier(thisObject->tokenizer, identifier);
        JackTokenizer_advance(thisObject->tokenizer);

        if (functionKind != SYMBOL_TABLE_KIND_NONE) {
            // token is varName
            char className[JACK_TOKEN_SIZE];
            SymbolTable_typeOf(thisObject->symbolTable, token, className);
            sprintf(functionName, "%s.%s", className, identifier);

            VMWriter_Segment segment;
            switch (SymbolTable_kindOf(thisObject->symbolTable, token))
            {
            case SYMBOL_TABLE_KIND_VAR:
                segment = VM_WRITER_SEGMENT_LOCAL;
                break;
            case SYMBOL_TABLE_KIND_ARG:
                segment = VM_WRITER_SEGMENT_ARG;
                break;
            case SYMBOL_TABLE_KIND_FIELD:
            default:
                segment = VM_WRITER_SEGMENT_THIS;
                break;
            }
            VMWriter_writePush(
                thisObject->vmWriter,
                segment,
                SymbolTable_indexOf(thisObject->symbolTable, token)
            );
            nArgs++;
        } else {
            // token is className
            sprintf(functionName, "%s.%s", token, identifier);
        }

        // '('
        JackTokenizer_symbol(thisObject->tokenizer, symbol);
    } else {
        // token is subroutineName (subroutine used)
        sprintf(functionName, "%s.%s", thisObject->className, token);

        VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_POINTER, 0);
        nArgs++;
    }
    JackTokenizer_advance(thisObject->tokenizer);

    nArgs += CompilationEngine_compileExpressionList(thisObject);

    // ...(省略)...

    VMWriter_writeCall(thisObject->vmWriter, functionName, nArgs);
    VMWriter_writePop(thisObject->vmWriter, VM_WRITER_SEGMENT_TEMP, 0);
}

CompilationEngine_compileLet

フィールド変数への代入に対応しました

11/JackCompiler4/CompilationEngine.c:L394-L450

void CompilationEngine_compileLet(CompilationEngine thisObject)
{
    // ...(省略)...

    CompilationEngine_compileExpression(thisObject);

    VMWriter_Segment segment;
    switch (kind)
    {
    case SYMBOL_TABLE_KIND_VAR:
        segment = VM_WRITER_SEGMENT_LOCAL;
        break;
    case SYMBOL_TABLE_KIND_ARG:
        segment = VM_WRITER_SEGMENT_ARG;
        break;
    case SYMBOL_TABLE_KIND_FIELD:
    default:
        segment = VM_WRITER_SEGMENT_THIS;
        break;
    }
    VMWriter_writePop(
        thisObject->vmWriter,
        segment,
        SymbolTable_indexOf(thisObject->symbolTable, varName)
    );

    // ...(省略)...
}

CompilationEngine_compileTerm

thisに対応しました
フィールド変数に対応しました
メソッド呼び出しの場合は第１引数にオブジェクトを指定するようにしました

11/JackCompiler4/CompilationEngine.c:L634-L796

void CompilationEngine_compileTerm(CompilationEngine thisObject)
{
    // ...(省略)...

    if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_INT_CONST) {
        // ...(省略)...
    } else if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_STRING_CONST) {
        // ...(省略)...
    } else if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_KEYWORD) {
        // ...(省略)...
        if (keyword == JACK_TOKENIZER_KEYWORD_THIS) {
            VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_POINTER, 0);
        }
    } else if (isSymbolToken(thisObject, "(")) {    // '(' expression ')'
        // ...(省略)...
    } else if (inSymbolListToken(thisObject, "-", "~", NULL)) { // unaryOp term
        // ...(省略)...
    } else {    // varName | varName '[' expression ']' | subroutineCall
        // ...(省略)...

        // '[' or '(' or '.' or not
        if (isSymbolToken(thisObject, "[")) {
            // ...(省略)...
        } else if (inSymbolListToken(thisObject, "(", ".", NULL)) {
            char functionName[JACK_TOKEN_SIZE];
            int nArgs = 0;

            // '(' or '.'
            JackTokenizer_symbol(thisObject->tokenizer, symbol);
            if (isSymbolToken(thisObject, ".")) {
                // token is (className | varName)
                JackTokenizer_advance(thisObject->tokenizer);

                // subroutineName (subroutine used)
                JackTokenizer_identifier(thisObject->tokenizer, identifier);
                JackTokenizer_advance(thisObject->tokenizer);

                if (kind != SYMBOL_TABLE_KIND_NONE) {
                    // token is varName
                    char className[JACK_TOKEN_SIZE];
                    SymbolTable_typeOf(thisObject->symbolTable, token, className);
                    sprintf(functionName, "%s.%s", className, identifier);

                    VMWriter_Segment segment;
                    switch (SymbolTable_kindOf(thisObject->symbolTable, token))
                    {
                    case SYMBOL_TABLE_KIND_VAR:
                        segment = VM_WRITER_SEGMENT_LOCAL;
                        break;
                    case SYMBOL_TABLE_KIND_ARG:
                        segment = VM_WRITER_SEGMENT_ARG;
                        break;
                    case SYMBOL_TABLE_KIND_FIELD:
                    default:
                        segment = VM_WRITER_SEGMENT_THIS;
                        break;
                    }
                    VMWriter_writePush(
                        thisObject->vmWriter,
                        segment,
                        SymbolTable_indexOf(thisObject->symbolTable, token)
                    );
                    nArgs++;
                } else {
                    // token is className
                    sprintf(functionName, "%s.%s", token, identifier);
                }

                // '('
                JackTokenizer_symbol(thisObject->tokenizer, symbol);
            } else {
                // token is subroutineName (subroutine used)
                sprintf(functionName, "%s.%s", thisObject->className, token);

                VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_POINTER, 0);
                nArgs++;
            }
            JackTokenizer_advance(thisObject->tokenizer);

            nArgs += CompilationEngine_compileExpressionList(thisObject);

            // ')'
            JackTokenizer_symbol(thisObject->tokenizer, symbol);
            JackTokenizer_advance(thisObject->tokenizer);

            VMWriter_writeCall(thisObject->vmWriter, functionName, nArgs);
        } else {
            // token is varName
            VMWriter_Segment segment;
            switch (kind)
            {
            case SYMBOL_TABLE_KIND_VAR:
                segment = VM_WRITER_SEGMENT_LOCAL;
                break;
            case SYMBOL_TABLE_KIND_ARG:
                segment = VM_WRITER_SEGMENT_ARG;
                break;
            case SYMBOL_TABLE_KIND_FIELD:
            default:
                segment = VM_WRITER_SEGMENT_THIS;
                break;
            }
            VMWriter_writePush(
                thisObject->vmWriter,
                segment,
                SymbolTable_indexOf(thisObject->symbolTable, token)
            );
        }
    }
}

配列と文字列

ソースコードは11/JackCompiler5/です。

ここでは下記を行いました。

配列と文字列に対応
テストコードの Average がコンパイルでき動作確認できるところを目指す

下記で使えます。

test11.sh:L98-L125

cp -r ./nand2tetris/projects/11/Seven 11/JackCompiler5/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler5/Seven/

cp -r ./nand2tetris/projects/11/ConvertToBin 11/JackCompiler5/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler5/ConvertToBin/

cp -r ./nand2tetris/projects/11/Square 11/JackCompiler5/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler5/Square/

cp -r ./nand2tetris/projects/11/Average 11/JackCompiler5/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler5/Average/

cd 11/JackCompiler5/

clang --std=c11 -Wall -Wextra -o JackCompiler main.c JackTokenizer.c JackTokenizerPrivate.c SymbolTable.c SymbolTablePrivate.c VMWriter.c CompilationEngine.c

./JackCompiler Seven
./JackCompiler ConvertToBin
./JackCompiler Square
./JackCompiler Average

cd -

# ./nand2tetris/tools/VMEmulator.sh
#   11/JackCompiler5/Seven
#   11/JackCompiler5/ConvertToBin
#   11/JackCompiler5/Square
#   11/JackCompiler5/Average

動かすためにOS提供関数の./nand2tetris/tools/OS/以下のファイルを使っています。
テストは自動実行できないので手動で確認する必要があります*6。

実行するとScreenエリアにプロンプトが現れて入力した数値の平均が計算されます。

CompilationEngineモジュール

CompilationEngine_compileLet

配列に対する代入に対応しました。expression結果の1時的な退避先としてtmpセグメントを使用しています。

11/JackCompiler5/CompilationEngine.c:L381-L439

void CompilationEngine_compileLet(CompilationEngine thisObject)
{
    // ...(省略)...

    // '[' or '='
    bool isArray = false;
    JackTokenizer_symbol(thisObject->tokenizer, symbol);
    if (isSymbolToken(thisObject, "[")) {
        // varName is Array
        isArray = true;
        JackTokenizer_advance(thisObject->tokenizer);

        // push index of array
        CompilationEngine_compileExpression(thisObject);
        // push varName
        VMWriter_writePush(
            thisObject->vmWriter,
            convertKindToSegment(kind),
            SymbolTable_indexOf(thisObject->symbolTable, varName)
        );
        // setup that segment 0 (1/2)
        VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_ADD);

        // ']'
        JackTokenizer_symbol(thisObject->tokenizer, symbol);
        JackTokenizer_advance(thisObject->tokenizer);

        // '='
        JackTokenizer_symbol(thisObject->tokenizer, symbol);
    }
    JackTokenizer_advance(thisObject->tokenizer);

    CompilationEngine_compileExpression(thisObject);

    if (isArray) {
        // setup that segment 0 (2/2)
        // pop expression result, pop, push expression result
        VMWriter_writePop(thisObject->vmWriter, VM_WRITER_SEGMENT_TEMP, 0);
        VMWriter_writePop(thisObject->vmWriter, VM_WRITER_SEGMENT_POINTER, 1);
        VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_TEMP, 0);
        VMWriter_writePop(thisObject->vmWriter, VM_WRITER_SEGMENT_THAT, 0);
    } else {
        VMWriter_writePop(
            thisObject->vmWriter,
            convertKindToSegment(kind),
            SymbolTable_indexOf(thisObject->symbolTable, varName)
        );
    }

    // ...(省略)...
}

CompilationEngine_compileTerm

文字列に対応しました。
配列への代入に対応しました。

11/JackCompiler5/CompilationEngine.c:L628-L778

void CompilationEngine_compileTerm(CompilationEngine thisObject)
{
    // ...(省略)...

    if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_INT_CONST) {
        // ...(省略)...
    } else if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_STRING_CONST) {
        // stringConstant
        JackTokenizer_stringVal(thisObject->tokenizer, stringVal);
        JackTokenizer_advance(thisObject->tokenizer);

        int length = strlen(stringVal);
        VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_CONST, length);
        VMWriter_writeCall(thisObject->vmWriter, "String.new", 1);
        for (int i = 0; i < length; i++) {
            VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_CONST, stringVal[i]);
            VMWriter_writeCall(thisObject->vmWriter, "String.appendChar", 2);
        }
    } else if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_KEYWORD) {
        // ...(省略)...
    } else if (isSymbolToken(thisObject, "(")) {    // '(' expression ')'
        // ...(省略)...
    } else if (inSymbolListToken(thisObject, "-", "~", NULL)) { // unaryOp term
        // ...(省略)...
    } else {    // varName | varName '[' expression ']' | subroutineCall
        // varName | subroutineName | className (used)
        char token[JACK_TOKEN_SIZE];
        JackTokenizer_identifier(thisObject->tokenizer, token);
        SymbolTable_Kind kind = SymbolTable_kindOf(thisObject->symbolTable, token);
        JackTokenizer_advance(thisObject->tokenizer);

        // '[' or '(' or '.' or not
        if (isSymbolToken(thisObject, "[")) {
            // token is Array of varName (varName[])
            JackTokenizer_symbol(thisObject->tokenizer, symbol);
            JackTokenizer_advance(thisObject->tokenizer);

            // push index of array
            CompilationEngine_compileExpression(thisObject);
            // push varName
            VMWriter_writePush(
                thisObject->vmWriter,
                convertKindToSegment(kind),
                SymbolTable_indexOf(thisObject->symbolTable, token)
            );
            // setup that segment 0
            VMWriter_writeArithmetic(thisObject->vmWriter, VM_WRITER_COMMAND_ADD);
            VMWriter_writePop(thisObject->vmWriter, VM_WRITER_SEGMENT_POINTER, 1);

            // ']'
            JackTokenizer_symbol(thisObject->tokenizer, symbol);
            JackTokenizer_advance(thisObject->tokenizer);

            VMWriter_writePush(thisObject->vmWriter, VM_WRITER_SEGMENT_THAT, 0);
        } else if (inSymbolListToken(thisObject, "(", ".", NULL)) {
        // ...(省略)...
        } else {
        // ...(省略)...
        }
    }
}

スタティック変数を含むオブジェクト

ソースコードは11/JackCompiler6/です。

ここでは下記を行いました。

スタティック変数に対応
テストコードの Pong がコンパイルでき動作確認できるところを目指す

下記で使えます。

test11.sh:L127-L164

cp -r ./nand2tetris/projects/11/Seven 11/JackCompiler6/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler6/Seven/

cp -r ./nand2tetris/projects/11/ConvertToBin 11/JackCompiler6/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler6/ConvertToBin/

cp -r ./nand2tetris/projects/11/Square 11/JackCompiler6/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler6/Square/

cp -r ./nand2tetris/projects/11/Average 11/JackCompiler6/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler6/Average/

cp -r ./nand2tetris/projects/11/Pong 11/JackCompiler6/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler6/Pong/

cp -r ./nand2tetris/projects/11/ComplexArrays 11/JackCompiler6/ && \
cp -r ./nand2tetris/tools/OS/* 11/JackCompiler6/ComplexArrays/

cd 11/JackCompiler6/

clang --std=c11 -Wall -Wextra -o JackCompiler main.c JackTokenizer.c JackTokenizerPrivate.c SymbolTable.c SymbolTablePrivate.c VMWriter.c CompilationEngine.c

./JackCompiler Seven
./JackCompiler ConvertToBin
./JackCompiler Square
./JackCompiler Average
./JackCompiler Pong
./JackCompiler ComplexArrays

cd -

# ./nand2tetris/tools/VMEmulator.sh
#   11/JackCompiler6/Seven
#   11/JackCompiler6/ConvertToBin
#   11/JackCompiler6/Square
#   11/JackCompiler6/Average
#   11/JackCompiler6/Pong
#   11/JackCompiler6/ComplexArrays

動かすためにOS提供関数の./nand2tetris/tools/OS/以下のファイルを使っています。
テストは自動実行できないので手動で確認する必要があります*7。

実行するとScreenエリアでPongゲームをプレイすることができます。

CompilationEngineモジュール

CompilationEngine_compileLet

スタティック変数に対応しました。

$ diff 11/JackCompiler5/CompilationEngine.c 11/JackCompiler6/CompilationEngine.c
903a904,906
>     case SYMBOL_TABLE_KIND_STATIC:
>         segment = VM_WRITER_SEGMENT_STATIC;
>         break;

配列の参照と式の評価

ソースコードは11/JackCompiler6/です。

変更はありません。テストコードの ComplexArrays はコンパイルでき動作確認できる状態です。

実行するとScreenエリアにテスト結果が表示されます。

まとめ

今回でようやくコンパイラは完成です。自作したコンパイラの結果が自作したCPUで動くのは嬉しいですね。ブログにまとめてあったおかげで前回から４年ほど時間が空いてますが記憶を取り戻して続きを進めることができました。C言語の実装についてはRustなどに書き換えたい気持ち。12章はオペレーティングシステムらしいですがたぶんシステムコール相当の関数をJack言語で実装していくみたいです。また気が向いたら進めたいです。

*1:前回から４年も経っている。。

*2:たまたま本棚にあった

*3:確認はNo animationにすること

*4:確認はNo animationにすること

*5:確認はNo animationにすること

*6:確認はNo animationにすること

*7:確認はNo animationにすること

2020-07-26

コンピュータシステムの理論と実装の10章のコンパイラ#1：構文解析を実装しました

コンピュータシステムの理論と実装 nand2tetris 字句解析構文解析 C言語

前回の続きです。今回はコンピュータシステムの理論と実装（以下、nand2tetris本）の10章のコンパイラ#1：構文解析をC言語で実装してみました。

今回のコード
概要
トークナイザ
- main.c (JackAnalyzerモジュール)
- JackTokenizerモジュール
パーサ
- 式を含まない版
- 完全版
まとめ

今回のコード

下記、タグv0.0.3になります。

github.com

下記で動かせます。

git clone -b v0.0.3 https://github.com/nihemak/nand2tetris.git
cd nand2tetris
# download nand2tetris environment
./setup.sh
# test all
./test.sh

概要

今回はコンパイラの構文解析部分です。実装は書籍にしたがって２段階で行いました。

.jackファイルまたは.jackファイル群を入力として受け取りそれぞれに対応する字句解析結果であるT.xmlファイルを生成するコマンドを実装
構文解析結果である.xmlファイルを生成するコマンドに改造

f:id:nihma:20200726191224p:plain

トークナイザ

ソースコードは10/JackAnalyzer/です。

ここでは字句解析を行い下記のトークンに分割しました。

トークン	概要
keyword	`class`, `method`, `function`, `constructor`, `int`, `boolean`, `char`, `void`, `var`, `static`, `field`, `let`, `do`, `if`, `else`, `while`, `return`, `true`, `false`, `null`, `this`
symbol	`{`, `}`, `(`, `)`, `[`, `]`, `.`, `,`, `;`, `+`, `-`, `*`, `/`, `&`, `\|`, `<`, `>`, `=`, `~`
identifier	数字以外から始まるアルファベット、数字、アンダースコアの文字列
integerConstant	0から32767
stringConstant	ダブルクォートで囲まれた文字列

下記で使えます。

test10.sh:L3-L19

cp -r ./nand2tetris/projects/10/Square 10/JackAnalyzer/ && \
mkdir -p 10/JackAnalyzer/Square/expect && \
mv 10/JackAnalyzer/Square/*.xml 10/JackAnalyzer/Square/expect/

# ...(省略)...

cd 10/JackAnalyzer/

clang --std=c11 -Wall -Wextra -o JackAnalyzer main.c JackTokenizer.c JackTokenizerPrivate.c

./JackAnalyzer Square

main.c (JackAnalyzerモジュール)

コマンドのエントリポイントです。書籍ではJackAnalyzerモジュールと呼ばれています。
main.cではコマンド引数の解析、JackTokenizerモジュールを用いた字句解析結果であるT.xmlファイルへの変換処理を行います。main.cの中で使う関数はmain.c内で下記のように定義しました。

10/JackAnalyzer/main.c:L10-L23

int analyzeByJackDir(DIR *dpJack, char *jackDirName);
int analyzeByJackFile(char *jackFileName);
int analyze(char *xmlFilePath, char *jackFilePath);
bool isJackFileName(char *jackFileName);
void createJackFilePath(char *jackDirName, char *jackFileName, char *jackFilePath);
void createXmlFilePathFromDirName(char *jackDirName, char *jackFileName, char *xmlFilePath);
void createXmlFilePathFromJackFileName(char *jackFileName, char *xmlFilePath);
void writeTokens(FILE *fp, JackTokenizer tokenizer);
void writeToken(FILE *fp, JackTokenizer tokenizer);
void writeKeyword(FILE *fp, JackTokenizer tokenizer);
void writeSymbol(FILE *fp, JackTokenizer tokenizer);
void writeIdentifier(FILE *fp, JackTokenizer tokenizer);
void writeIntegerConstant(FILE *fp, JackTokenizer tokenizer);
void writeStringConstant(FILE *fp, JackTokenizer tokenizer);

コマンド引数には.jackファイルまたはjackファイルを複数含むディレクトリにいづれかを指定できます。関数はanalyzeByJackDirおよびanalyzeByJackFileです。この処理は前回のバーチャルマシンでの実装とほぼ同じです。ただし出力が１ファイルのバーチャルマシンと違いこちらは.jackに対して一対一に対応する.xmlを出力します。

変換処理の実装は下記の通りです。JackTokenizerモジュールを使用して.xmlを作成します。

10/JackAnalyzer/main.c:L127-L150

int analyze(char *xmlFilePath, char *jackFilePath)
{
    FILE *fpJack, *fpXml;
    JackTokenizer tokenizer;

    if ((fpJack = fopen(jackFilePath, "r")) == NULL) {
        fprintf(stderr, "Error: jack file not found (%s)\n", jackFilePath);
        return 1;
    }

    if ((fpXml = fopen(xmlFilePath, "w")) == NULL) {
        fprintf(stderr, "Error: xml file not open (%s)\n", xmlFilePath);
        fclose(fpJack);
        return 1;
    }

    tokenizer = JackTokenizer_init(fpJack);
    writeTokens(fpXml, tokenizer);

    fclose(fpXml);
    fclose(fpJack);

    return 0;
}

.xmlへのタグの書き込みは下記の通りです。.xmlなので<, >, &はそれぞれ<, >, &"に変換しました。

10/JackAnalyzer/main.c:L197-L309

void writeTokens(FILE *fp, JackTokenizer tokenizer)
{
    fprintf(fp, "<tokens>\n");
    while (JackTokenizer_hasMoreTokens(tokenizer)) {
        JackTokenizer_advance(tokenizer);
        writeToken(fp, tokenizer);
    }
    fprintf(fp, "</tokens>\n");
}

void writeToken(FILE *fp, JackTokenizer tokenizer)
{
    switch (JackTokenizer_tokenType(tokenizer))
    {
    case JACK_TOKENIZER_TOKEN_TYPE_KEYWORD:
        writeKeyword(fp, tokenizer);
        break;
    case JACK_TOKENIZER_TOKEN_TYPE_SYMBOL:
        writeSymbol(fp, tokenizer);
        break;
    case JACK_TOKENIZER_TOKEN_TYPE_IDENTIFIER:
        writeIdentifier(fp, tokenizer);
        break;
    case JACK_TOKENIZER_TOKEN_TYPE_INT_CONST:
        writeIntegerConstant(fp, tokenizer);
        break;
    case JACK_TOKENIZER_TOKEN_TYPE_STRING_CONST:
        writeStringConstant(fp, tokenizer);
        break; 
    default:
        break;
    }
}

void writeKeyword(FILE *fp, JackTokenizer tokenizer)
{
    struct keyword {
        JackTokenizer_Keyword id;
        char *string;
    };
    struct keyword keywords[] = {
        { JACK_TOKENIZER_KEYWORD_CLASS,        "class" },
        { JACK_TOKENIZER_KEYWORD_METHOD,       "method" },
        { JACK_TOKENIZER_KEYWORD_FUNCTION,     "function" },
        { JACK_TOKENIZER_KEYWORD_CONSTRUCTION, "constructor" },
        { JACK_TOKENIZER_KEYWORD_INT,          "int" },
        { JACK_TOKENIZER_KEYWORD_BOOLEAN,      "boolean" },
        { JACK_TOKENIZER_KEYWORD_CHAR,         "char" },
        { JACK_TOKENIZER_KEYWORD_VOID,         "void" },
        { JACK_TOKENIZER_KEYWORD_VAR,          "var" },
        { JACK_TOKENIZER_KEYWORD_STATIC,       "static" },
        { JACK_TOKENIZER_KEYWORD_FIELD,        "field" },
        { JACK_TOKENIZER_KEYWORD_LET,          "let" },
        { JACK_TOKENIZER_KEYWORD_DO,           "do" },
        { JACK_TOKENIZER_KEYWORD_IF,           "if" },
        { JACK_TOKENIZER_KEYWORD_ELSE,         "else" },
        { JACK_TOKENIZER_KEYWORD_WHILE,        "while" },
        { JACK_TOKENIZER_KEYWORD_RETURN,       "return" },
        { JACK_TOKENIZER_KEYWORD_TRUE,         "true" },
        { JACK_TOKENIZER_KEYWORD_FALSE,        "false" },
        { JACK_TOKENIZER_KEYWORD_NULL,         "null" },
        { JACK_TOKENIZER_KEYWORD_THIS,         "this" },
    };
    JackTokenizer_Keyword id = JackTokenizer_keyword(tokenizer);

    fprintf(fp, "<keyword> ");
    for (size_t i = 0; i < sizeof(keywords) / sizeof(keywords[0]); i++) {
        if (id == keywords[i].id) {
            fprintf(fp, "%s", keywords[i].string);
            break;
        }
    }
    fprintf(fp, " </keyword>\n");
}

void writeSymbol(FILE *fp, JackTokenizer tokenizer)
{
    char token[JACK_TOKEN_SIZE];
    JackTokenizer_symbol(tokenizer, token);

    fprintf(fp, "<symbol> ");
    if (strcmp(token, "<") == 0) {
        fprintf(fp, "&lt;");
    } else if (strcmp(token, ">") == 0) {
        fprintf(fp, "&gt;");
    } else if (strcmp(token, "&") == 0) {
        fprintf(fp, "&amp;");
    } else {
        fprintf(fp, "%s", token);
    }
    fprintf(fp, " </symbol>\n");
}

void writeIdentifier(FILE *fp, JackTokenizer tokenizer)
{
    char token[JACK_TOKEN_SIZE];
    JackTokenizer_identifier(tokenizer, token);
    fprintf(fp, "<identifier> %s </identifier>\n", token);
}

void writeIntegerConstant(FILE *fp, JackTokenizer tokenizer)
{
    int intVal;
    JackTokenizer_intVal(tokenizer, &intVal);
    fprintf(fp, "<integerConstant> %d </integerConstant>\n", intVal);
}

void writeStringConstant(FILE *fp, JackTokenizer tokenizer)
{
    char token[JACK_TOKEN_SIZE];
    JackTokenizer_stringVal(tokenizer, token);
    fprintf(fp, "<stringConstant> %s </stringConstant>\n", token);
}

JackTokenizerモジュール

.jackファイルを字句解析するためのモジュールです。
main.cで利用する関数はJackTokenizer.hで下記のように定義しました。jack_tokenizer構造体はtypedefして定義はJackTokenizer.c内に隠蔽するようにしてオブジェクトとして使うようにしました。それぞれの実装はJackTokenizer.cで行いました。

10/JackAnalyzer/JackTokenizer.h:L9-L53

typedef enum {
    JACK_TOKENIZER_TOKEN_TYPE_KEYWORD = 1,
    JACK_TOKENIZER_TOKEN_TYPE_SYMBOL,
    JACK_TOKENIZER_TOKEN_TYPE_IDENTIFIER,
    JACK_TOKENIZER_TOKEN_TYPE_INT_CONST,
    JACK_TOKENIZER_TOKEN_TYPE_STRING_CONST,
    JACK_TOKENIZER_TOKEN_TYPE_STRING_UNKNOWN
} JackTokenizer_TokenType;

typedef enum {
    JACK_TOKENIZER_KEYWORD_CLASS = 1,
    JACK_TOKENIZER_KEYWORD_METHOD,
    JACK_TOKENIZER_KEYWORD_FUNCTION,
    JACK_TOKENIZER_KEYWORD_CONSTRUCTION,
    JACK_TOKENIZER_KEYWORD_INT,
    JACK_TOKENIZER_KEYWORD_BOOLEAN,
    JACK_TOKENIZER_KEYWORD_CHAR,
    JACK_TOKENIZER_KEYWORD_VOID,
    JACK_TOKENIZER_KEYWORD_VAR,
    JACK_TOKENIZER_KEYWORD_STATIC,
    JACK_TOKENIZER_KEYWORD_FIELD,
    JACK_TOKENIZER_KEYWORD_LET,
    JACK_TOKENIZER_KEYWORD_DO,
    JACK_TOKENIZER_KEYWORD_IF,
    JACK_TOKENIZER_KEYWORD_ELSE,
    JACK_TOKENIZER_KEYWORD_WHILE,
    JACK_TOKENIZER_KEYWORD_RETURN,
    JACK_TOKENIZER_KEYWORD_TRUE,
    JACK_TOKENIZER_KEYWORD_FALSE,
    JACK_TOKENIZER_KEYWORD_NULL,
    JACK_TOKENIZER_KEYWORD_THIS,
    JACK_TOKENIZER_KEYWORD_UNKNOWN
} JackTokenizer_Keyword;

typedef struct jack_tokenizer * JackTokenizer;

JackTokenizer JackTokenizer_init(FILE *fpJack);
bool JackTokenizer_hasMoreTokens(JackTokenizer thisObject);
void JackTokenizer_advance(JackTokenizer thisObject);
JackTokenizer_TokenType JackTokenizer_tokenType(JackTokenizer thisObject);
JackTokenizer_Keyword JackTokenizer_keyword(JackTokenizer thisObject);
void JackTokenizer_symbol(JackTokenizer thisObject, char *symbol);
void JackTokenizer_identifier(JackTokenizer thisObject, char *identifier);
void JackTokenizer_intVal(JackTokenizer thisObject, int *intVal);
void JackTokenizer_stringVal(JackTokenizer thisObject, char *stringVal);

またJackTokenizer.c内で使う関数はJackTokenizerPrivate.hで下記のように定義しJackTokenizerPrivate.cで実装しました。

10/JackAnalyzer/JackTokenizerPrivate.h:L7-L12

void moveNextToken(FILE *fp);
bool isEndOfFile(FILE *fp);
bool getTokenSymbol(FILE *fp, char *token);
bool getTokenStringConstant(FILE *fp, char *token);
bool getTokenIntConstant(FILE *fp, char *token);
bool getTokenIdentifierOrKeyword(FILE *fp, char *token);

現在のトークンの種類やキーワードの場合のキーワードの種類の判断はJackTokenizer_advance関数で行いました。

10/JackAnalyzer/JackTokenizer.c:L36-L56

void JackTokenizer_advance(JackTokenizer thisObject)
{
    thisObject->keyword = JACK_TOKENIZER_KEYWORD_UNKNOWN;
    if (getTokenSymbol(thisObject->fpJack, thisObject->token)) {
        thisObject->type = JACK_TOKENIZER_TOKEN_TYPE_SYMBOL;
    } else if (getTokenStringConstant(thisObject->fpJack, thisObject->token)) {
        thisObject->type = JACK_TOKENIZER_TOKEN_TYPE_STRING_CONST;
    } else if (getTokenIntConstant(thisObject->fpJack, thisObject->token)) {
        thisObject->type = JACK_TOKENIZER_TOKEN_TYPE_INT_CONST;
    } else {
        getTokenIdentifierOrKeyword(thisObject->fpJack, thisObject->token);

        thisObject->keyword = convertIdentifierToKeyword(thisObject->token);
        if (thisObject->keyword == JACK_TOKENIZER_KEYWORD_UNKNOWN) {
            thisObject->type = JACK_TOKENIZER_TOKEN_TYPE_IDENTIFIER;
        } else {
            thisObject->type = JACK_TOKENIZER_TOKEN_TYPE_KEYWORD;
        }
    }
    moveNextToken(thisObject->fpJack);
}

キーワードの種類の文字列をJackTokenizer_Keyword定数に変換する処理は下記の通りです。

10/JackAnalyzer/JackTokenizer.c:L96-L131

JackTokenizer_Keyword convertIdentifierToKeyword(char *token)
{
    struct keyword {
        JackTokenizer_Keyword id;
        char *string;
    };
    struct keyword keywords[] = {
        { JACK_TOKENIZER_KEYWORD_CLASS,        "class" },
        { JACK_TOKENIZER_KEYWORD_METHOD,       "method" },
        { JACK_TOKENIZER_KEYWORD_FUNCTION,     "function" },
        { JACK_TOKENIZER_KEYWORD_CONSTRUCTION, "constructor" },
        { JACK_TOKENIZER_KEYWORD_INT,          "int" },
        { JACK_TOKENIZER_KEYWORD_BOOLEAN,      "boolean" },
        { JACK_TOKENIZER_KEYWORD_CHAR,         "char" },
        { JACK_TOKENIZER_KEYWORD_VOID,         "void" },
        { JACK_TOKENIZER_KEYWORD_VAR,          "var" },
        { JACK_TOKENIZER_KEYWORD_STATIC,       "static" },
        { JACK_TOKENIZER_KEYWORD_FIELD,        "field" },
        { JACK_TOKENIZER_KEYWORD_LET,          "let" },
        { JACK_TOKENIZER_KEYWORD_DO,           "do" },
        { JACK_TOKENIZER_KEYWORD_IF,           "if" },
        { JACK_TOKENIZER_KEYWORD_ELSE,         "else" },
        { JACK_TOKENIZER_KEYWORD_WHILE,        "while" },
        { JACK_TOKENIZER_KEYWORD_RETURN,       "return" },
        { JACK_TOKENIZER_KEYWORD_TRUE,         "true" },
        { JACK_TOKENIZER_KEYWORD_FALSE,        "false" },
        { JACK_TOKENIZER_KEYWORD_NULL,         "null" },
        { JACK_TOKENIZER_KEYWORD_THIS,         "this" },
    };
    for (size_t i = 0; i < sizeof(keywords) / sizeof(keywords[0]); i++) {
        if (strcmp(token, keywords[i].string) == 0) {
            return keywords[i].id;
        }
    }
    return JACK_TOKENIZER_KEYWORD_UNKNOWN;
}

それぞれ実装の詳細はソースコードを参照。

パーサ

ここでは下記の通りJack言語の文法に従い構文解析処理の実装を行いました。各実装はCompilationEngineモジュールを参照。

CompilationEngine_compileClass関数
- class: 'class' className '{' classVarDec* subroutineDec* '}'
CompilationEngine_compileClassVarDec関数
- classVarDec: ('static' | 'field') type varName (',' varName)* ';'
CompilationEngine_compileSubroutine関数
- subroutineDec: ('constructor' | 'function' | 'method') ('void' | type) subroutineName '(' parameterList ')' subroutineBody
- subroutineBody: '{' varDec* statements '}'
CompilationEngine_compileParameterList関数
- parameterList: ((type varName) (',' type varName)*)?
CompilationEngine_compileVarDec関数
- varDec: 'var' type varName (',' varName)* ';'
CompilationEngine_compileStatements関数
- statements: statement*
- statement: letStatement | ifStatement | whileStatement | doStatement | returnStatement
CompilationEngine_compileDo関数
- doStatement: 'do' subroutineCall ';'
- subroutineCall: subroutineName '(' expressionList ')' | (className | varName) '.' subroutineName '(' expressionList ')'
CompilationEngine_compileLet関数
- letStatement: 'let' varName ('[' expression ']')? '=' expression ';'
CompilationEngine_compileWhile関数
- whileStatement: 'while' '(' expression ')' '{' statements '}'
CompilationEngine_compileReturn関数
- returnStatement: 'return' expression? ';'
CompilationEngine_compileIf関数
- ifStatement: 'if' '(' expression ')' '{' statements '}' ('else' '{' statements '}')?
CompilationEngine_compileExpression関数
- expression: term (op term)*
- op: '+' | '-' | '*' | '/' | '&' | '|' | '<' | '>' | '='
CompilationEngine_compileTerm関数
- term: integerConstant | stringConstant | keywordConstant | varName | varName '[' expression ']' | subroutineCall | '(' expression ')' | unaryOp term
- subroutineCall: subroutineName '(' expressionList ')' | (className | varName) '.' subroutineName '(' expressionList ')'
- unaryOp: '-' | '~'
CompilationEngine_compileExpressionList関数
- expressionList: (expression (',' expression)*)?

式を含まない版

ソースコードは10/JackAnalyzer2/です。

ここではJack言語の文法のうちCompilationEngine_compileTerm以外について実装しました。

下記で使えます。

test10.sh:L34-L42

cp -r ./nand2tetris/projects/10/ExpressionLessSquare 10/JackAnalyzer2/ && \
mkdir -p 10/JackAnalyzer2/ExpressionLessSquare/expect && \
mv 10/JackAnalyzer2/ExpressionLessSquare/*.xml 10/JackAnalyzer2/ExpressionLessSquare/expect/

cd 10/JackAnalyzer2/

clang --std=c11 -Wall -Wextra -o JackAnalyzer main.c JackTokenizer.c JackTokenizerPrivate.c CompilationEngine.c

./JackAnalyzer ExpressionLessSquare

main.c (JackAnalyzerモジュール)

下記の変更を行いました。

生成する.xmlファイルの名前をXxxT.xmlからXxx.xmlに変更
analyze関数をCompilationEngineモジュールを用いるように変更
writeXXX関数を削除（CompilationEngineモジュールへ移動）

差分は下記の通りです。

$ diff 10/JackAnalyzer/main.c 10/JackAnalyzer2/main.c 
1c1
< #include "JackTokenizer.h"
---
> #include "CompilationEngine.h"
2a3
> #include <stdbool.h>
7c8
< #define XML_FILENAME_MAX_LENGTH JACK_FILENAME_MAX_LENGTH  // length('.jack') - length('T.xml') = 0
---
> #define XML_FILENAME_MAX_LENGTH (JACK_FILENAME_MAX_LENGTH - 1)  // length('.jack') - length('.xml') = 1
17,23d17
< void writeTokens(FILE *fp, JackTokenizer tokenizer);
< void writeToken(FILE *fp, JackTokenizer tokenizer);
< void writeKeyword(FILE *fp, JackTokenizer tokenizer);
< void writeSymbol(FILE *fp, JackTokenizer tokenizer);
< void writeIdentifier(FILE *fp, JackTokenizer tokenizer);
< void writeIntegerConstant(FILE *fp, JackTokenizer tokenizer);
< void writeStringConstant(FILE *fp, JackTokenizer tokenizer);
130c124
<     JackTokenizer tokenizer;
---
>     CompilationEngine compilationEngine;
143,144c137,138
<     tokenizer = JackTokenizer_init(fpJack);
<     writeTokens(fpXml, tokenizer);
---
>     compilationEngine = CompilationEngine_init(fpJack, fpXml);
>     CompilationEngine_compileClass(compilationEngine);
180c174
<     // xmlFilePath is {jackDirName}/{jackFileName} - ".jack" + "T.xml"
---
>     // xmlFilePath is {jackDirName}/{jackFileName} - ".jack" + ".xml"
184c178
<     strcat(xmlFilePath, "T.xml");
---
>     strcat(xmlFilePath, ".xml");
189c183
<     // XmlFilePath is {jackFileName} - ".jack" + "T.xml"
---
>     // XmlFilePath is {jackFileName} - ".jack" + ".xml"
194,308c188
<     strcat(xmlFilePath, "T.xml");
< }
< 
< void writeTokens(FILE *fp, JackTokenizer tokenizer)
< {
<     fprintf(fp, "<tokens>\n");
<     while (JackTokenizer_hasMoreTokens(tokenizer)) {
<         JackTokenizer_advance(tokenizer);
<         writeToken(fp, tokenizer);
<     }
<     fprintf(fp, "</tokens>\n");
< }
< 
< void writeToken(FILE *fp, JackTokenizer tokenizer)
< {
<     switch (JackTokenizer_tokenType(tokenizer))
<     {
<     case JACK_TOKENIZER_TOKEN_TYPE_KEYWORD:
<         writeKeyword(fp, tokenizer);
<         break;
<     case JACK_TOKENIZER_TOKEN_TYPE_SYMBOL:
<         writeSymbol(fp, tokenizer);
<         break;
<     case JACK_TOKENIZER_TOKEN_TYPE_IDENTIFIER:
<         writeIdentifier(fp, tokenizer);
<         break;
<     case JACK_TOKENIZER_TOKEN_TYPE_INT_CONST:
<         writeIntegerConstant(fp, tokenizer);
<         break;
<     case JACK_TOKENIZER_TOKEN_TYPE_STRING_CONST:
<         writeStringConstant(fp, tokenizer);
<         break; 
<     default:
<         break;
<     }
< }
< 
< void writeKeyword(FILE *fp, JackTokenizer tokenizer)
< {
<     struct keyword {
<         JackTokenizer_Keyword id;
<         char *string;
<     };
<     struct keyword keywords[] = {
<         { JACK_TOKENIZER_KEYWORD_CLASS,        "class" },
<         { JACK_TOKENIZER_KEYWORD_METHOD,       "method" },
<         { JACK_TOKENIZER_KEYWORD_FUNCTION,     "function" },
<         { JACK_TOKENIZER_KEYWORD_CONSTRUCTION, "constructor" },
<         { JACK_TOKENIZER_KEYWORD_INT,          "int" },
<         { JACK_TOKENIZER_KEYWORD_BOOLEAN,      "boolean" },
<         { JACK_TOKENIZER_KEYWORD_CHAR,         "char" },
<         { JACK_TOKENIZER_KEYWORD_VOID,         "void" },
<         { JACK_TOKENIZER_KEYWORD_VAR,          "var" },
<         { JACK_TOKENIZER_KEYWORD_STATIC,       "static" },
<         { JACK_TOKENIZER_KEYWORD_FIELD,        "field" },
<         { JACK_TOKENIZER_KEYWORD_LET,          "let" },
<         { JACK_TOKENIZER_KEYWORD_DO,           "do" },
<         { JACK_TOKENIZER_KEYWORD_IF,           "if" },
<         { JACK_TOKENIZER_KEYWORD_ELSE,         "else" },
<         { JACK_TOKENIZER_KEYWORD_WHILE,        "while" },
<         { JACK_TOKENIZER_KEYWORD_RETURN,       "return" },
<         { JACK_TOKENIZER_KEYWORD_TRUE,         "true" },
<         { JACK_TOKENIZER_KEYWORD_FALSE,        "false" },
<         { JACK_TOKENIZER_KEYWORD_NULL,         "null" },
<         { JACK_TOKENIZER_KEYWORD_THIS,         "this" },
<     };
<     JackTokenizer_Keyword id = JackTokenizer_keyword(tokenizer);
< 
<     fprintf(fp, "<keyword> ");
<     for (size_t i = 0; i < sizeof(keywords) / sizeof(keywords[0]); i++) {
<         if (id == keywords[i].id) {
<             fprintf(fp, "%s", keywords[i].string);
<             break;
<         }
<     }
<     fprintf(fp, " </keyword>\n");
< }
< 
< void writeSymbol(FILE *fp, JackTokenizer tokenizer)
< {
<     char token[JACK_TOKEN_SIZE];
<     JackTokenizer_symbol(tokenizer, token);
< 
<     fprintf(fp, "<symbol> ");
<     if (strcmp(token, "<") == 0) {
<         fprintf(fp, "&lt;");
<     } else if (strcmp(token, ">") == 0) {
<         fprintf(fp, "&gt;");
<     } else if (strcmp(token, "&") == 0) {
<         fprintf(fp, "&amp;");
<     } else {
<         fprintf(fp, "%s", token);
<     }
<     fprintf(fp, " </symbol>\n");
< }
< 
< void writeIdentifier(FILE *fp, JackTokenizer tokenizer)
< {
<     char token[JACK_TOKEN_SIZE];
<     JackTokenizer_identifier(tokenizer, token);
<     fprintf(fp, "<identifier> %s </identifier>\n", token);
< }
< 
< void writeIntegerConstant(FILE *fp, JackTokenizer tokenizer)
< {
<     int intVal;
<     JackTokenizer_intVal(tokenizer, &intVal);
<     fprintf(fp, "<integerConstant> %d </integerConstant>\n", intVal);
< }
< 
< void writeStringConstant(FILE *fp, JackTokenizer tokenizer)
< {
<     char token[JACK_TOKEN_SIZE];
<     JackTokenizer_stringVal(tokenizer, token);
<     fprintf(fp, "<stringConstant> %s </stringConstant>\n", token);
---
>     strcat(xmlFilePath, ".xml");

JackTokenizerモジュール

変更はありません。

$ diff 10/JackAnalyzer/JackTokenizer.h 10/JackAnalyzer2/JackTokenizer.h 
$ diff 10/JackAnalyzer/JackTokenizer.c 10/JackAnalyzer2/JackTokenizer.c 
$ diff 10/JackAnalyzer/JackTokenizerPrivate.h 10/JackAnalyzer2/JackTokenizerPrivate.h
$ diff 10/JackAnalyzer/JackTokenizerPrivate.c 10/JackAnalyzer2/JackTokenizerPrivate.c

CompilationEngineモジュール

.jackファイルを構文解析して.xmlファイルに出力するためのモジュールです。
main.cで利用する関数はCompilationEngine.hで下記のように定義しました。compilation_engine構造体はtypedefして定義はCompilationEngine.c内に隠蔽するようにしてオブジェクトとして使うようにしました。それぞれの実装はCompilationEngine.cで行いました。

10/JackAnalyzer2/CompilationEngine.h:L6-L22

typedef struct compilation_engine * CompilationEngine;

CompilationEngine CompilationEngine_init(FILE *fpJack, FILE *fpXml);
void CompilationEngine_compileClass(CompilationEngine thisObject);
void CompilationEngine_compileClassVarDec(CompilationEngine thisObject);
void CompilationEngine_compileSubroutine(CompilationEngine thisObject);
void CompilationEngine_compileParameterList(CompilationEngine thisObject);
void CompilationEngine_compileVarDec(CompilationEngine thisObject);
void CompilationEngine_compileStatements(CompilationEngine thisObject);
void CompilationEngine_compileDo(CompilationEngine thisObject);
void CompilationEngine_compileLet(CompilationEngine thisObject);
void CompilationEngine_compileWhile(CompilationEngine thisObject);
void CompilationEngine_compileReturn(CompilationEngine thisObject);
void CompilationEngine_compileIf(CompilationEngine thisObject);
void CompilationEngine_compileExpression(CompilationEngine thisObject);
void CompilationEngine_compileTerm(CompilationEngine thisObject);
void CompilationEngine_compileExpressionList(CompilationEngine thisObject);

またCompilationEngine.c内で使う関数は下記の通りです。writeXXX関数はmain.cから移動してきました。

10/JackAnalyzer2/CompilationEngine.c:L6-L15

void writeToken(FILE *fp, JackTokenizer tokenizer);
void writeKeyword(FILE *fp, JackTokenizer tokenizer);
void writeSymbol(FILE *fp, JackTokenizer tokenizer);
void writeIdentifier(FILE *fp, JackTokenizer tokenizer);
void writeIntegerConstant(FILE *fp, JackTokenizer tokenizer);
void writeStringConstant(FILE *fp, JackTokenizer tokenizer);
void advanceAndWriteToken(CompilationEngine thisObject);
bool isKeywordToken(CompilationEngine thisObject, JackTokenizer_Keyword keyword);
bool isSymbolToken(CompilationEngine thisObject, char *symbol);
bool inSymbolListToken(CompilationEngine thisObject, ...);

Jack言語の文法にしたがって構文解析して.xmlファイルに出力する実装は下記の通りです。ほぼLL(1)文法であるため割とシンプルです。なお、CompilationEngine_compileTermだけは次節で実装するためきちんとした実装にはなっていません。

10/JackAnalyzer2/CompilationEngine.c:L34-L359

// 'class' className '{' classVarDec* subroutineDec* '}'
void CompilationEngine_compileClass(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<class>\n");

    advanceAndWriteToken(thisObject);   // 'class'
    advanceAndWriteToken(thisObject);   // className
    advanceAndWriteToken(thisObject);   // '{'

    JackTokenizer_advance(thisObject->tokenizer);   // '}' or not
    while (! isSymbolToken(thisObject, "}")) {
        if (
            isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_STATIC) ||
            isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_FIELD)
        ) {  // classVarDec
            CompilationEngine_compileClassVarDec(thisObject);
        } else if (
            isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_CONSTRUCTION) ||
            isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_FUNCTION) ||
            isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_METHOD)
        ) {  // subroutineDec
            CompilationEngine_compileSubroutine(thisObject);
        } else {
            break;
        }
    }
    writeToken(thisObject->fpXml ,thisObject->tokenizer);    // '}'

    fprintf(thisObject->fpXml, "</class>\n");
}

// ('static' | 'field') type varName (',' varName)* ';'
void CompilationEngine_compileClassVarDec(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<classVarDec>\n");

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ('static' | 'field')
    advanceAndWriteToken(thisObject);   // type

    do {
        advanceAndWriteToken(thisObject);   // varName
        advanceAndWriteToken(thisObject);   // ',' or ';'
    } while (! isSymbolToken(thisObject, ";"));

    fprintf(thisObject->fpXml, "</classVarDec>\n");

    JackTokenizer_advance(thisObject->tokenizer);
}

// ('constructor' | 'function' | 'method') ('void' | type) subroutineName '(' parameterList ')' subroutineBody
// subroutineBody: '{' varDec* statements '}'
void CompilationEngine_compileSubroutine(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<subroutineDec>\n");

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ('constructor' | 'function' | 'method')
    advanceAndWriteToken(thisObject);   // ('void' | type)
    advanceAndWriteToken(thisObject);   // subroutineName
    advanceAndWriteToken(thisObject);   // '('

    JackTokenizer_advance(thisObject->tokenizer);
    CompilationEngine_compileParameterList(thisObject);

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ')'

    fprintf(thisObject->fpXml, "<subroutineBody>\n");

    advanceAndWriteToken(thisObject);   // '{'

    JackTokenizer_advance(thisObject->tokenizer);   // 'var' or statements or '}'
    while (isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_VAR)) {
        CompilationEngine_compileVarDec(thisObject);
    }
    if (! isSymbolToken(thisObject, "}")) {   // statements or '}'
        CompilationEngine_compileStatements(thisObject);
    }
    writeToken(thisObject->fpXml, thisObject->tokenizer);   // '}'

    fprintf(thisObject->fpXml, "</subroutineBody>\n");

    fprintf(thisObject->fpXml, "</subroutineDec>\n");

    JackTokenizer_advance(thisObject->tokenizer);
}

// ((type varName) (',' type varName)*)?
void CompilationEngine_compileParameterList(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<parameterList>\n");

    if (JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_KEYWORD) {  // type
        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // type
        advanceAndWriteToken(thisObject);   // varName

        JackTokenizer_advance(thisObject->tokenizer);   // ',' or not
        while (isSymbolToken(thisObject, ",")) {
            writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ','
            advanceAndWriteToken(thisObject);   // type
            advanceAndWriteToken(thisObject);   // varName
            JackTokenizer_advance(thisObject->tokenizer);   // ',' or not
        }
    }

    fprintf(thisObject->fpXml, "</parameterList>\n");
}

// 'var' type varName (',' varName)* ';'
void CompilationEngine_compileVarDec(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<varDec>\n");

    writeToken(thisObject->fpXml, thisObject->tokenizer);   // 'var'
    advanceAndWriteToken(thisObject);   // type

    do {
        advanceAndWriteToken(thisObject);   // varName
        advanceAndWriteToken(thisObject);   // ',' or ';'
    } while (! isSymbolToken(thisObject, ";"));

    fprintf(thisObject->fpXml, "</varDec>\n");

    JackTokenizer_advance(thisObject->tokenizer);
}

// statement*
// statement: letStatement | ifStatement | whileStatement | doStatement | returnStatement
void CompilationEngine_compileStatements(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<statements>\n");

    do {
        if (isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_LET)) {
            CompilationEngine_compileLet(thisObject);
        } else if (isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_IF)) {
            CompilationEngine_compileIf(thisObject);
        } else if (isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_WHILE)) {
            CompilationEngine_compileWhile(thisObject);
        } else if (isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_DO)) {
            CompilationEngine_compileDo(thisObject);
        } else if (isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_RETURN)) {
            CompilationEngine_compileReturn(thisObject);
        } else {
            break;
        }
    } while (true);

    fprintf(thisObject->fpXml, "</statements>\n");
}

// 'do' subroutineCall ';'
// subroutineCall: subroutineName '(' expressionList ')' | (className | varName) '.' subroutineName '(' expressionList ')'
void CompilationEngine_compileDo(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<doStatement>\n");

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // 'do'

    advanceAndWriteToken(thisObject);   // subroutineName | (className | varName)
    advanceAndWriteToken(thisObject);   // '(' or '.'
    if (isSymbolToken(thisObject, ".")) {
        advanceAndWriteToken(thisObject);   // subroutineName
        advanceAndWriteToken(thisObject);   // '('
    }

    JackTokenizer_advance(thisObject->tokenizer);
    CompilationEngine_compileExpressionList(thisObject);

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ')'
    advanceAndWriteToken(thisObject);   // ';'

    fprintf(thisObject->fpXml, "</doStatement>\n");

    JackTokenizer_advance(thisObject->tokenizer);
}

// 'let' varName ('[' expression ']')? '=' expression ';'
void CompilationEngine_compileLet(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<letStatement>\n");

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // 'let'
    advanceAndWriteToken(thisObject);   // varName
    advanceAndWriteToken(thisObject);   // '[' or '='
    if (isSymbolToken(thisObject, "[")) {
        JackTokenizer_advance(thisObject->tokenizer);
        CompilationEngine_compileExpression(thisObject);

        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ']'
        advanceAndWriteToken(thisObject);   // '='
    }

    JackTokenizer_advance(thisObject->tokenizer);
    CompilationEngine_compileExpression(thisObject);

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ';'

    fprintf(thisObject->fpXml, "</letStatement>\n");

    JackTokenizer_advance(thisObject->tokenizer);
}

// 'while' '(' expression ')' '{' statements '}'
void CompilationEngine_compileWhile(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<whileStatement>\n");

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // 'while'
    advanceAndWriteToken(thisObject);   // '('

    JackTokenizer_advance(thisObject->tokenizer);
    CompilationEngine_compileExpression(thisObject);

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ')'
    advanceAndWriteToken(thisObject);   // '{'

    JackTokenizer_advance(thisObject->tokenizer);
    CompilationEngine_compileStatements(thisObject);

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // '}'

    fprintf(thisObject->fpXml, "</whileStatement>\n");

    JackTokenizer_advance(thisObject->tokenizer);
}

// 'return' expression? ';'
void CompilationEngine_compileReturn(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<returnStatement>\n");

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // 'return'

    JackTokenizer_advance(thisObject->tokenizer);   // expression or ';'
    if (! isSymbolToken(thisObject, ";")) {
        CompilationEngine_compileExpression(thisObject);
    }
    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ';'

    fprintf(thisObject->fpXml, "</returnStatement>\n");

    JackTokenizer_advance(thisObject->tokenizer);
}

// 'if' '(' expression ')' '{' statements '}' ('else' '{' statements '}')?
void CompilationEngine_compileIf(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<ifStatement>\n");

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // 'if'
    advanceAndWriteToken(thisObject);   // '('

    JackTokenizer_advance(thisObject->tokenizer);
    CompilationEngine_compileExpression(thisObject);

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ')'
    advanceAndWriteToken(thisObject);   // '{'

    JackTokenizer_advance(thisObject->tokenizer);
    CompilationEngine_compileStatements(thisObject);

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // '}'

    JackTokenizer_advance(thisObject->tokenizer);   // 'else' or not
    if (isKeywordToken(thisObject, JACK_TOKENIZER_KEYWORD_ELSE)) {
        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // 'else'
        advanceAndWriteToken(thisObject);   // '{'

        JackTokenizer_advance(thisObject->tokenizer);
        CompilationEngine_compileStatements(thisObject);

        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // '}'

        JackTokenizer_advance(thisObject->tokenizer);
    }

    fprintf(thisObject->fpXml, "</ifStatement>\n");
}

// term (op term)*
// op: '+' | '-' | '*' | '/' | '&' | '|' | '<' | '>' | '='
void CompilationEngine_compileExpression(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<expression>\n");

    CompilationEngine_compileTerm(thisObject);

    while (inSymbolListToken(thisObject, "+", "-", "*",  "/", "&", "|", "<", ">", "=", NULL)) {
        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // op

        JackTokenizer_advance(thisObject->tokenizer);
        CompilationEngine_compileTerm(thisObject);
    }

    fprintf(thisObject->fpXml, "</expression>\n");
}

// integerConstant | stringConstant | keywordConstant | varName | varName '[' expression ']' | subroutineCall | '(' expression ')' | unaryOp term
void CompilationEngine_compileTerm(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<term>\n");

    writeToken(thisObject->fpXml ,thisObject->tokenizer);   // term

    fprintf(thisObject->fpXml, "</term>\n");

    JackTokenizer_advance(thisObject->tokenizer);
}

// (expression (',' expression)*)?
void CompilationEngine_compileExpressionList(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<expressionList>\n");

    if (! isSymbolToken(thisObject, ")")) { // expression is not ')'
        CompilationEngine_compileExpression(thisObject);

        while (isSymbolToken(thisObject, ",")) {
            writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ','

            JackTokenizer_advance(thisObject->tokenizer);   // expression
            CompilationEngine_compileExpression(thisObject);
        }
    }

    fprintf(thisObject->fpXml, "</expressionList>\n");
}

それぞれ実装の詳細はソースコードを参照。

完全版

ソースコードは10/JackAnalyzer3/です。

ここではJack言語の文法のCompilationEngine_compileTermを実装しました。

下記で使えます。

test10.sh:L51-L67

cp -r ./nand2tetris/projects/10/Square 10/JackAnalyzer3/ && \
mkdir -p 10/JackAnalyzer3/Square/expect && \
mv 10/JackAnalyzer3/Square/*.xml 10/JackAnalyzer3/Square/expect/

# ...(省略)...

cd 10/JackAnalyzer3/

clang --std=c11 -Wall -Wextra -o JackAnalyzer main.c JackTokenizer.c JackTokenizerPrivate.c CompilationEngine.c

./JackAnalyzer Square

main.c (JackAnalyzerモジュール)

変更はありません。

$ diff 10/JackAnalyzer2/main.c 10/JackAnalyzer3/main.c

JackTokenizerモジュール

変更はありません。

$ diff 10/JackAnalyzer2/JackTokenizer.h 10/JackAnalyzer3/JackTokenizer.h 
$ diff 10/JackAnalyzer2/JackTokenizer.c 10/JackAnalyzer3/JackTokenizer.c 
$ diff 10/JackAnalyzer2/JackTokenizerPrivate.h 10/JackAnalyzer3/JackTokenizerPrivate.h
$ diff 10/JackAnalyzer2/JackTokenizerPrivate.c 10/JackAnalyzer3/JackTokenizerPrivate.c

CompilationEngineモジュール

CompilationEngine_compileTerm関数を実装しました。

10/JackAnalyzer3/CompilationEngine.c:L330-L388

// integerConstant | stringConstant | keywordConstant | varName | varName '[' expression ']' | subroutineCall | '(' expression ')' | unaryOp term
// subroutineCall: subroutineName '(' expressionList ')' | (className | varName) '.' subroutineName '(' expressionList ')'
// unaryOp: '-' | '~'
void CompilationEngine_compileTerm(CompilationEngine thisObject)
{
    fprintf(thisObject->fpXml, "<term>\n");

    if (
        JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_INT_CONST ||
        JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_STRING_CONST ||
        JackTokenizer_tokenType(thisObject->tokenizer) == JACK_TOKENIZER_TOKEN_TYPE_KEYWORD
    ) { // integerConstant | stringConstant | keywordConstant
        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // integerConstant or stringConstant or keywordConstant
        JackTokenizer_advance(thisObject->tokenizer);
    } else if (isSymbolToken(thisObject, "(")) {    // '(' expression ')'
        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // '('

        JackTokenizer_advance(thisObject->tokenizer);
        CompilationEngine_compileExpression(thisObject);

        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ')'

        JackTokenizer_advance(thisObject->tokenizer);
    } else if (inSymbolListToken(thisObject, "-", "~", NULL)) { // unaryOp term
        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // unaryOp

        JackTokenizer_advance(thisObject->tokenizer);
        CompilationEngine_compileTerm(thisObject);
    } else {    // varName | varName '[' expression ']' | subroutineCall
        writeToken(thisObject->fpXml ,thisObject->tokenizer);   // varName | subroutineName | className

        JackTokenizer_advance(thisObject->tokenizer);   // '[' or '(' or '.' or not
        if (isSymbolToken(thisObject, "[")) {
            writeToken(thisObject->fpXml ,thisObject->tokenizer);

            JackTokenizer_advance(thisObject->tokenizer);
            CompilationEngine_compileExpression(thisObject);

            writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ']'

            JackTokenizer_advance(thisObject->tokenizer);
        } else if (inSymbolListToken(thisObject, "(", ".", NULL)) {
            writeToken(thisObject->fpXml ,thisObject->tokenizer);   // '(' or '.'

            if (isSymbolToken(thisObject, ".")) {
                advanceAndWriteToken(thisObject);   // subroutineName
                advanceAndWriteToken(thisObject);   // '('
            }
            JackTokenizer_advance(thisObject->tokenizer);
            CompilationEngine_compileExpressionList(thisObject);

            writeToken(thisObject->fpXml ,thisObject->tokenizer);   // ')'

            JackTokenizer_advance(thisObject->tokenizer);
        }
    }

    fprintf(thisObject->fpXml, "</term>\n");
}

まとめ

今回はJack言語の文法にしたがった構文解析器を実装しました。11章は今回の構文解析器を改造してコード生成を行えるようにしてコンパイラを完成させるようです。11章にはシンボルテーブルのテストが用意されていなかったりテストプログラムが目視テストだったりと大変そうですが時間があれば挑んでみたいです。

2020-06-13

コンピュータシステムの理論と実装の7章と8章のバーチャルマシンを実装しました

コンピュータシステムの理論と実装 nand2tetris バーチャルマシンスタックアセンブラ C言語

前回の続きです。今回はコンピュータシステムの理論と実装（以下、nand2tetris本）の7章と8章のバーチャルマシンをC言語で実装してみました。

今回のコード
概要
7章（スタック操作）
- スタック算術コマンド
- メモリアクセスコマンド
8章（プログラム制御）
まとめ

今回のコード

下記、タグv0.0.2になります。

github.com

下記で動かせます。

git clone -b v0.0.2 https://github.com/nihemak/nand2tetris.git
cd nand2tetris
# download nand2tetris environment
./setup.sh
# test all
./test.sh

概要

今回、実装したのは.vmファイルまたは.vmファイル群を入力として受け取り.asmファイルを生成するコマンドです。

f:id:nihma:20200613174708p:plain

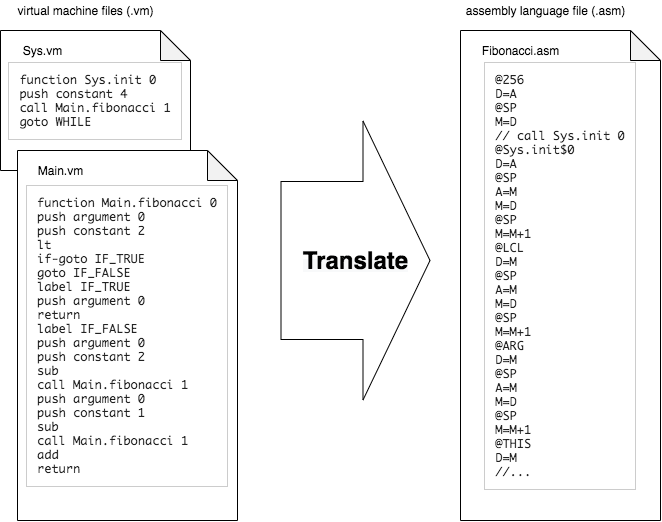
バーチャルマシンはスタックベースです。長くなってしまうためここでは細かい仕様の説明は省略します。気になる場合はコンピュータシステムの理論と実装の7章と8章に詳しく記載されています。この記事の目的は自分が後から思い出すためのとっかかりを残すことであるため実装してみた内容の概要の記述にとどめます。

なお、実装は書籍が用意したテストプログラムに対応する形でインクリメンタルに進めました。そのため、次の５つのバージョンが存在し後になるほど高機能になっていきます。

スタック算術コマンドに対応
メモリアクセスコマンドに対応
プログラムフローコマンドに対応
関数呼び出しコマンド（ブートストラップなし）に対応
関数呼び出しコマンド（完全版）に対応

7章（スタック操作）

スタック算術コマンド

ソースコードは07/VMtranslator1/です。

ここでは下記のコマンドに対応しました。

コマンド	概要
add	pop y, pop x, push (x + y)
sub	pop y, pop x, push (x - y)
neg	pop y, push (-y)
eq	pop y, pop x, push (x == y ? -1(true/0xFFFF) : 0(false/0x0000))
gt	pop y, pop x, push (x > y ? -1(true/0xFFFF) : 0(false/0x0000))
lt	pop y, pop x, push (x < y ? -1(true/0xFFFF) : 0(false/0x0000))
and	pop y, pop x, push (x and y)
or	pop y, pop x, push (x or y)
not	pop y, push (not y)
push constant index	push index

下記で使えます。

test07.sh:L3-L16

cp ./nand2tetris/projects/07/StackArithmetic/SimpleAdd/* 07/VMtranslator1/

# ...(省略)...

cd 07/VMtranslator1/

clang --std=c11 -Wall -Wextra -o VMtranslator main.c Parser.c ParserPrivate.c CodeWriter.c CodeWriterPrivate.c

./VMtranslator SimpleAdd.vm

main.c

コマンドのエントリポイントです。
main.cではコマンド引数の解析、ParserモジュールおよびCodeモジュールを用いたアセンブラへの変換処理を行います。main.cの中で使う関数はmain.c内で下記のように定義しました。

07/VMtranslator1/main.c:L15-L21

int translateByVmDir(DIR *dpVm, char *vmDirName);
int translateByVmFile(char *vmFileName);
bool isVmFileName(char *vmFileName);
void createVmFilePath(char *vmDirName, char *vmFileName, char *vmFilePath);
void createAsmFilePathFromDirName(char *vmDirName, char *asmFilePath);
void createAsmFilePathFromVmFileName(char *vmFileName, char *asmFilePath);
void translate(Parser parser, CodeWriter codeWriter);

コマンド引数には.vmファイルまたは.vmファイルを複数含むディレクトリにいづれかを指定できます。ただし複数の.vmファイルに対応するのは最後になるためここでは1ファイルのみ処理するようにしました。

ディレクトリが指定された場合の処理は次の通りです。.asmファイルを作成し.vmファイルが見つかったら変換処理(translate関数)に引き渡しています。ただしファイル数分ループしていますが1ファイル処理したらbreakで抜けるようにしてあります。

07/VMtranslator1/main.c:L54-L125

int translateByVmDir(DIR *dpVm, char *vmDirName)
{
    char asmFilePath[VM_DIRNAME_MAX_LENGTH + ASM_FILENAME_MAX_LENGTH + 1];
    char vmFilePath[VM_DIRNAME_MAX_LENGTH + VM_FILENAME_MAX_LENGTH + 1];
    int vmFileNum = 0;
    FILE *fpVm, *fpAsm;
    struct dirent *dEntry;
    Parser parser;
    CodeWriter codeWriter;

    if (strlen(vmDirName) > VM_DIRNAME_MAX_LENGTH) {
        fprintf(
            stderr, 
            "Error: Vm dirname max size is invalid. Max size is %d. (%s) is %lu\n", 
            VM_DIRNAME_MAX_LENGTH, 
            vmDirName,
            strlen(vmDirName)
        );
        return 1;
    }

    createAsmFilePathFromDirName(vmDirName, asmFilePath);
    if ((fpAsm = fopen(asmFilePath, "w")) == NULL) {
        fprintf(stderr, "Error: asm file not open (%s)\n", asmFilePath);
        return 1;
    }
    codeWriter = CodeWriter_init(fpAsm);

    while ((dEntry = readdir(dpVm)) != NULL) {
        char *vmFileName = dEntry->d_name;
        if (dEntry->d_type != DT_REG) {  // not file
            continue;
        }
        if (! isVmFileName(vmFileName)) {
            continue;
        }
        if (strlen(vmFileName) > VM_FILENAME_MAX_LENGTH) {
            fprintf(
                stderr, 
                "Skip: Vm filename max size is invalid. Max size is %d. (%s) is %lu\n", 
                VM_FILENAME_MAX_LENGTH, 
                vmFileName,
                strlen(vmFileName)
            );
            continue;
        }
        vmFileNum++;

        createVmFilePath(vmDirName, vmFileName, vmFilePath);
        if ((fpVm = fopen(vmFilePath, "r")) == NULL) {
            fprintf(stderr, "Error: vm file not found (%s)\n", vmFilePath);
            CodeWriter_close(codeWriter);
            return 1;
        }
        CodeWriter_setFileName(codeWriter, vmFileName);

        parser = Parser_init(fpVm);
        translate(parser, codeWriter);

        fclose(fpVm);

        break;
    }
    CodeWriter_close(codeWriter);

    if (vmFileNum == 0) {
        fprintf(stderr, "Error: vm file not found\n");
        return 1;
    }

    return 0;
}

ファイルが指定された場合の処理は次の通りです。.asmファイルを作成し変換処理(translate関数)に引き渡しています。

07/VMtranslator1/main.c:L127-L171

int translateByVmFile(char *vmFileName)
{
    char asmFilePath[ASM_FILENAME_MAX_LENGTH];
    FILE *fpVm, *fpAsm;
    Parser parser;
    CodeWriter codeWriter;

    if (! isVmFileName(vmFileName)) {
        fprintf(stderr, "Error: Vm filename extension(.vm) is invalid. (%s)\n", vmFileName);
        return 1;
    }

    if (strlen(vmFileName) > VM_FILENAME_MAX_LENGTH) {
        fprintf(
            stderr, 
            "Error: Vm filename max size is invalid. Max size is %d. (%s) is %lu\n", 
            VM_FILENAME_MAX_LENGTH, 
            vmFileName,
            strlen(vmFileName)
        );
        return 1;
    }

    if ((fpVm = fopen(vmFileName, "r")) == NULL) {
        fprintf(stderr, "Error: vm file not found (%s)\n", vmFileName);
        return 1;
    }
    parser = Parser_init(fpVm);

    createAsmFilePathFromVmFileName(vmFileName, asmFilePath);
    if ((fpAsm = fopen(asmFilePath, "w")) == NULL) {
        fprintf(stderr, "Error: asm file not open (%s)\n", asmFilePath);
        fclose(fpVm);
        return 1;
    }
    codeWriter = CodeWriter_init(fpAsm);

    CodeWriter_setFileName(codeWriter, vmFileName);
    translate(parser, codeWriter);

    CodeWriter_close(codeWriter);
    fclose(fpVm);

    return 0;
}

変換処理の実装は下記の通りです。.vmファイルをParserモジュールでパースしつつcommandTypeに応じてCodeWriterモジュールで対応するアセンブリ処理を.asmファイルに追記しています。

07/VMtranslator1/main.c:L219-L239

void translate(Parser parser, CodeWriter codeWriter)
{
    char command[PARSER_COMMAND_MAX_LENGTH + 1];
    char segment[PARSER_ARG1_MAX_LENGTH + 1];

    while (Parser_hasMoreCommands(parser)) {
        Parser_advance(parser);
        switch (Parser_commandType(parser)) {
        case PARSER_COMMAND_TYPE_C_ARITHMETIC:
            Parser_arg1(parser, command);
            CodeWriter_writeArithmetic(codeWriter, command);
            break;
        case PARSER_COMMAND_TYPE_C_PUSH:
            Parser_arg1(parser, segment);
            CodeWriter_writePushPop(codeWriter, Parser_commandType(parser), segment, Parser_arg2(parser));
            break;
        default:
            break;
        }
    }
}

Parserモジュール

.vmファイルをパースするためのモジュールです。
main.cで利用する関数はParser.hで下記のように定義しました。parser構造体はtypedefして定義はParser.c内に隠蔽するようにしてオブジェクトとして使うようにしました。それぞれの実装はParser.cで行いました。

07/VMtranslator1/Parser.h:L11-L23

typedef enum {
    PARSER_COMMAND_TYPE_C_ARITHMETIC = 1,
    PARSER_COMMAND_TYPE_C_PUSH
} Parser_CommandType;

typedef struct parser * Parser;

Parser Parser_init(FILE *fpVm);
bool Parser_hasMoreCommands(Parser thisObject);
void Parser_advance(Parser thisObject);
Parser_CommandType Parser_commandType(Parser thisObject);
void Parser_arg1(Parser thisObject, char *arg1);
int Parser_arg2(Parser thisObject);

またParser.c内で使う関数はParserPrivate.hで下記のように定義しParserPrivate.cで実装しました。

07/VMtranslator1/ParserPrivate.h:L7-L16

bool isSpace(FILE *fpVm);
bool isComment(FILE *fpVm);
bool isEndOfFile(FILE *fpVm);
bool isEndOfLine(FILE *fpVm);
bool isToken(FILE *fpVm);
void skipSpaces(FILE *fpVm);
void skipEndOFLines(FILE *fpVm);
void skipComment(FILE *fpVm);
void moveNextAdvance(FILE *fpVm);
void getToken(FILE *fpVm, char *token);

各コマンドごとの処理は下記の通りです。

07/VMtranslator1/Parser.c:L55-L86

Parser_CommandType Parser_commandType(Parser thisObject)
{
    IF_CMP_RET(thisObject->command,  "add", PARSER_COMMAND_TYPE_C_ARITHMETIC);
    IF_CMP_RET(thisObject->command,  "sub", PARSER_COMMAND_TYPE_C_ARITHMETIC);   
    IF_CMP_RET(thisObject->command,  "neg", PARSER_COMMAND_TYPE_C_ARITHMETIC);
    IF_CMP_RET(thisObject->command,   "eq", PARSER_COMMAND_TYPE_C_ARITHMETIC);
    IF_CMP_RET(thisObject->command,   "gt", PARSER_COMMAND_TYPE_C_ARITHMETIC);
    IF_CMP_RET(thisObject->command,   "lt", PARSER_COMMAND_TYPE_C_ARITHMETIC);
    IF_CMP_RET(thisObject->command,  "and", PARSER_COMMAND_TYPE_C_ARITHMETIC);
    IF_CMP_RET(thisObject->command,   "or", PARSER_COMMAND_TYPE_C_ARITHMETIC);
    IF_CMP_RET(thisObject->command,  "not", PARSER_COMMAND_TYPE_C_ARITHMETIC);
    IF_CMP_RET(thisObject->command, "push", PARSER_COMMAND_TYPE_C_PUSH);

    return -1;
}

void Parser_arg1(Parser thisObject, char *arg1)
{
    if (Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_ARITHMETIC) {
        strcpy(arg1, thisObject->command);
    } else if (Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_PUSH) {
        strcpy(arg1, thisObject->arg1);
    }
}

int Parser_arg2(Parser thisObject)
{
    if (Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_PUSH) {
        return atoi(thisObject->arg2);
    }
    return -1;
}

それぞれ実装の詳細はソースコードを参照。

CodeWriterモジュール

コマンドに対応するアセンブリ処理を.asmファイルに追記するためのモジュールです。
main.cで利用する関数はCodeWriter.hで下記のように定義しました。code_writer構造体はtypedefして定義はCodeWriter.c内に隠蔽するようにしてオブジェクトとして使うようにしました。それぞれの実装はCodeWriter.cで行いました。

07/VMtranslator1/CodeWriter.h:L9-L20

typedef struct code_writer * CodeWriter;

CodeWriter CodeWriter_init(FILE *fpAsm);
void CodeWriter_setFileName(CodeWriter thisObject, char *fileName);
void CodeWriter_writeArithmetic(CodeWriter thisObject, char *command);
void CodeWriter_writePushPop(
    CodeWriter thisObject,
    Parser_CommandType command,
    char *segment,
    int index
);
void CodeWriter_close(CodeWriter thisObject);

またCodeWriter.c内で使う関数はCodeWriterPrivate.hで下記のように定義しCodeWriterPrivate.cで実装しました。

07/VMtranslator1/CodeWriterPrivate.h:L8-L16

void fputslist(FILE* fp, ...);

void writeArithmethicAdd(FILE* fpAsm);
void writeArithmethicSub(FILE* fpAsm);
void writeArithmethicNeg(FILE* fpAsm);
void writeArithmethicEq(FILE* fpAsm, char *skipLabel);
void writeArithmethicGt(FILE* fpAsm, char *skipLabel);
void writeArithmethicLt(FILE* fpAsm, char *skipLabel);
void writeArithmethicAnd(FILE* fpAsm);
void writeArithmethicOr(FILE* fpAsm);
void writeArithmethicNot(FILE* fpAsm);

void writePushConstant(FILE* fpAsm, int index);

長くなってしまうため詳細は省きますが例えばaddの実装は下記の通り、対応するアセンブリ処理をfputsで追記しているだけです。fputslist関数は自作のfputsを連続して呼び出す関数です。

07/VMtranslator1/CodeWriterPrivate.c:L11-

// pop y, pop x, push (x + y)
void writeArithmethicAdd(FILE* fpAsm) { writeArithmethicBinaryOperation(fpAsm, "D+M"); }

// ...(省略)...

// Binary operation (M <- x, D <- y)
void writeArithmethicBinaryOperation(FILE* fpAsm, char *comp)
{
    fputslist(
        fpAsm,
        "// BinaryOperation ", comp, "\n",
        // Memory[SP] -= 1
        "@SP\n",
        "M=M-1\n",
        // y <- Memory[Memory[SP]]
        "A=M\n",
        "D=M\n",
        // Memory[SP] -= 1
        "@SP\n",
        "M=M-1\n",
        // x <- Memory[Memory[SP]]
        "A=M\n",
        // Memory[Memory[SP]] <- comp
        "M=", comp, "\n",
        // Memory[SP] += 1
        "@SP\n",
        "M=M+1\n",
        NULL
    );
}

// ...(省略)...

void fputslist(FILE* fp, ...)
{
    char* string;

    va_list args;
    va_start(args, fp);

    while ((string = va_arg(args, char*)) != NULL) {
        fputs(string, fp);
    }

    va_end(args);
}

それぞれ実装の詳細はソースコードを参照。

メモリアクセスコマンド

ソースコードは07/VMtranslator2/です。

ここでは下記のコマンドに対応しました。

コマンド	概要
push local index	push Memory[Memory[LCL]+index]
pop local index	pop Memory[Memory[LCL]+index]
push argument index	push Memory[Memory[ARG]+index]
pop argument index	pop Memory[Memory[ARG]+index]
push this index	push Memory[Memory[THIS]+index]
pop this index	pop Memory[Memory[THIS]+index]
push that index	push Memory[Memory[THAT]+index]
pop that index	pop Memory[Memory[THAT]+index]
push pointer index	push R{3+index}
pop pointer index	pop R{3+index}
push temp index	push R{5+index}
pop temp index	pop R{5+index}
push static index	push Memory[vmFileName.index]
pop static index	pop Memory[vmFileName.index]

下記で使えます。

test07.sh:L20-L40

cp ./nand2tetris/projects/07/MemoryAccess/BasicTest/* 07/VMtranslator2/

# ...(省略)...

cd 07/VMtranslator2/

clang --std=c11 -Wall -Wextra -o VMtranslator main.c Parser.c ParserPrivate.c CodeWriter.c CodeWriterPrivate.c

# ...(省略)...
./VMtranslator BasicTest.vm

main.c

popに対応しました。

$ diff -r 07/VMtranslator1/main.c 07/VMtranslator2/main.c 
231a232
>         case PARSER_COMMAND_TYPE_C_POP:

Parserモジュール

popに対応しました。

$ diff -r 07/VMtranslator1/Parser.h 07/VMtranslator2/Parser.h 
13c13,14
<     PARSER_COMMAND_TYPE_C_PUSH
---
>     PARSER_COMMAND_TYPE_C_PUSH,
>     PARSER_COMMAND_TYPE_C_POP
$ diff -r 07/VMtranslator1/Parser.c 07/VMtranslator2/Parser.c
40a41
>     case PARSER_COMMAND_TYPE_C_POP:
66a68
>     IF_CMP_RET(thisObject->command,  "pop", PARSER_COMMAND_TYPE_C_POP);
75c77
<     } else if (Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_PUSH) {
---
>     } else {
82c84,85
<     if (Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_PUSH) {
---
>     if (Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_PUSH ||
>         Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_POP) {
$ diff -r 07/VMtranslator1/ParserPrivate.h 07/VMtranslator2/ParserPrivate.h
$ diff -r 07/VMtranslator1/ParserPrivate.c 07/VMtranslator2/ParserPrivate.c

CodeWriterモジュール

constant以外のpushとpopに対応しました。

$ diff -w -r 07/VMtranslator1/CodeWriter.h 07/VMtranslator2/CodeWriter.h 
$ diff -w -r 07/VMtranslator1/CodeWriter.c 07/VMtranslator2/CodeWriter.c
57,60c57,78
<     if (command == PARSER_COMMAND_TYPE_C_PUSH) {
<         if (strcmp(segment, "constant") == 0) {
<             writePushConstant(thisObject->fpAsm, index);
<         }
---
>     switch (command) {
>     case PARSER_COMMAND_TYPE_C_PUSH:
>              if (strcmp(segment, "constant") == 0) writePushConstant(thisObject->fpAsm, index);
>         else if (strcmp(segment,    "local") == 0) writePushLocal(thisObject->fpAsm, index);
>         else if (strcmp(segment, "argument") == 0) writePushArgument(thisObject->fpAsm, index);
>         else if (strcmp(segment,     "this") == 0) writePushThis(thisObject->fpAsm, index);
>         else if (strcmp(segment,     "that") == 0) writePushThat(thisObject->fpAsm, index);
>         else if (strcmp(segment,  "pointer") == 0) writePushPointer(thisObject->fpAsm, index);
>         else if (strcmp(segment,     "temp") == 0) writePushTemp(thisObject->fpAsm, index);
>         else if (strcmp(segment,   "static") == 0) writePushStatic(thisObject->fpAsm, thisObject->vmFileName, index);
>         break;
>     case PARSER_COMMAND_TYPE_C_POP:
>              if (strcmp(segment,    "local") == 0) writePopLocal(thisObject->fpAsm, index);
>         else if (strcmp(segment, "argument") == 0) writePopArgument(thisObject->fpAsm, index);
>         else if (strcmp(segment,     "this") == 0) writePopThis(thisObject->fpAsm, index);
>         else if (strcmp(segment,     "that") == 0) writePopThat(thisObject->fpAsm, index);
>         else if (strcmp(segment,  "pointer") == 0) writePopPointer(thisObject->fpAsm, index);
>         else if (strcmp(segment,     "temp") == 0) writePopTemp(thisObject->fpAsm, index);
>         else if (strcmp(segment,   "static") == 0) writePopStatic(thisObject->fpAsm, thisObject->vmFileName, index);
>         break;
>     default:
>         break;
$ diff -w -r 07/VMtranslator1/CodeWriterPrivate.h 07/VMtranslator2/CodeWriterPrivate.h
18a19,32
> void writePushLocal(FILE* fpAsm, int index);
> void writePopLocal(FILE* fpAsm, int index);
> void writePushArgument(FILE* fpAsm, int index);
> void writePopArgument(FILE* fpAsm, int index);
> void writePushThis(FILE* fpAsm, int index);
> void writePopThis(FILE* fpAsm, int index);
> void writePushThat(FILE* fpAsm, int index);
> void writePopThat(FILE* fpAsm, int index);
> void writePushPointer(FILE* fpAsm, int index);
> void writePopPointer(FILE* fpAsm, int index);
> void writePushTemp(FILE* fpAsm, int index);
> void writePopTemp(FILE* fpAsm, int index);
> void writePushStatic(FILE* fpAsm, char *vmFileName, int index);
> void writePopStatic(FILE* fpAsm, char *vmFileName, int index);
$ diff -w -r 07/VMtranslator1/CodeWriterPrivate.c 07/VMtranslator2/CodeWriterPrivate.c
1a2
> #include "CodeWriter.h"
4c5,6
< #define PUSH_CONSTANT_INDEX_MAX_DIGIT (6)
---
> #define PUSH_POP_INDEX_MAX_DIGIT   (6)
> #define PUSH_POP_SYMBOL_MAX_LENGTH (CODE_WRITER_VM_FILENAME_MAX_LENGTH + PUSH_POP_INDEX_MAX_DIGIT + 1)
9a12,16
> void writePushSymbol(FILE* fpAsm, char *symbol, int index);
> void writePopSymbol(FILE* fpAsm, char *symbol, int index);
> void writePushRegister(FILE* fpAsm, int registerNumber);
> void writePopRegister(FILE* fpAsm, int registerNumber);
> 
34c41
<     char indexStr[PUSH_CONSTANT_INDEX_MAX_DIGIT + 1];
---
>     char indexStr[PUSH_POP_INDEX_MAX_DIGIT + 1];
52a60,131
> // push Memory[Memory[LCL]+index]
> void writePushLocal(FILE* fpAsm, int index) { writePushSymbol(fpAsm, "LCL", index); }
> // pop Memory[Memory[LCL]+index]
> void writePopLocal(FILE* fpAsm, int index)  { writePopSymbol(fpAsm, "LCL", index); }
> 
> // push Memory[Memory[ARG]+index]
> void writePushArgument(FILE* fpAsm, int index) { writePushSymbol(fpAsm, "ARG", index); }
> // pop Memory[Memory[ARG]+index]
> void writePopArgument(FILE* fpAsm, int index)  { writePopSymbol(fpAsm, "ARG", index); }
> 
> // push Memory[Memory[THIS]+index]
> void writePushThis(FILE* fpAsm, int index) { writePushSymbol(fpAsm, "THIS", index); }
> // pop Memory[Memory[THIS]+index]
> void writePopThis(FILE* fpAsm, int index)  { writePopSymbol(fpAsm, "THIS", index); }
> 
> // push Memory[Memory[THAT]+index]
> void writePushThat(FILE* fpAsm, int index) { writePushSymbol(fpAsm, "THAT", index); }
> // pop Memory[Memory[THAT]+index]
> void writePopThat(FILE* fpAsm, int index)  { writePopSymbol(fpAsm, "THAT", index); }
> 
> // push R{3+index}
> void writePushPointer(FILE* fpAsm, int index) { writePushRegister(fpAsm, 3 + index); }
> // pop R{3+index}
> void writePopPointer(FILE* fpAsm, int index)  { writePopRegister(fpAsm, 3 + index); }
> 
> // push R{5+index}
> void writePushTemp(FILE* fpAsm, int index) { writePushRegister(fpAsm, 5 + index); }
> // pop R{5+index}
> void writePopTemp(FILE* fpAsm, int index)  { writePopRegister(fpAsm, 5 + index); }
> 
> // push Memory[vmFileName.index]
> void writePushStatic(FILE* fpAsm, char *vmFileName, int index)
> {
>     char symbol[PUSH_POP_SYMBOL_MAX_LENGTH + 1];
>     sprintf(symbol, "%s.%d", vmFileName, index);
> 
>     fputslist(
>         fpAsm,
>         // Memory[Memory[SP]] <- Memory[symbol]
>         "@", symbol, "\n",
>         "D=M\n",
>         "@SP\n",
>         "A=M\n",
>         "M=D\n",
>         // Memory[SP] += 1
>         "@SP\n",
>         "M=M+1\n",
>         NULL
>     );
> }
> 
> // pop Memory[vmFileName.index]
> void writePopStatic(FILE* fpAsm, char *vmFileName, int index)
> {
>     char symbol[PUSH_POP_SYMBOL_MAX_LENGTH + 1];
>     sprintf(symbol, "%s.%d", vmFileName, index);
> 
>     fputslist(
>         fpAsm,
>         // Memory[SP] -= 1
>         "@SP\n",
>         "M=M-1\n",
>         // Memory[symbol] <- Memory[Memory[SP]]
>         "@SP\n",
>         "A=M\n",
>         "D=M\n",
>         "@", symbol, "\n",
>         "M=D\n",
>         NULL
>     );
> }
> 
137a217,316
> // push Memory[Memory[Symbol]+index]
> void writePushSymbol(FILE* fpAsm, char *symbol, int index)
> {
>     char indexStr[PUSH_POP_INDEX_MAX_DIGIT + 1];
>     sprintf(indexStr, "%d", index);
> 
>     fputslist(
>         fpAsm,
>         "// push symbol ", symbol, " ", indexStr, "\n",
>         // R13 <- Memory[Symbol]+index
>         "@", indexStr, "\n",
>         "D=A\n",
>         "@", symbol, "\n",
>         "D=D+M\n",
>         "@R13\n",
>         "M=D\n",
>         // Memory[Memory[SP]] <- Memory[R13] 
>         "A=M\n",
>         "D=M\n",
>         "@SP\n",
>         "A=M\n",
>         "M=D\n",
>         // Memory[SP] += 1
>         "@SP\n",
>         "M=M+1\n",
>         NULL
>     );
> }
> 
> // pop Memory[Memory[Symbol]+index]
> void writePopSymbol(FILE* fpAsm, char *symbol, int index)
> {
>     char indexStr[PUSH_POP_INDEX_MAX_DIGIT + 1];
>     sprintf(indexStr, "%d", index);
> 
>     fputslist(
>         fpAsm,
>         // Memory[SP] -= 1
>         "@SP\n",
>         "M=M-1\n",
>         // R13 <- Memory[Symbol]+index
>         "@", indexStr, "\n",
>         "D=A\n",
>         "@", symbol, "\n",
>         "D=D+M\n",
>         "@R13\n",
>         "M=D\n",
>         // Memory[R13] <- Memory[Memory[SP]]
>         "@SP\n",
>         "A=M\n",
>         "D=M\n",
>         "@R13\n",
>         "A=M\n",
>         "M=D\n",
>         NULL
>     );
> }
> 
> // push R{registerNumber}
> void writePushRegister(FILE* fpAsm, int registerNumber)
> {
>     char symbol[8];
>     sprintf(symbol, "R%d", registerNumber);
> 
>     fputslist(
>         fpAsm,
>         // Memory[Memory[SP]] <- register
>         "@", symbol, "\n",
>         "D=M\n",
>         "@SP\n",
>         "A=M\n",
>         "M=D\n",
>         // Memory[SP] += 1
>         "@SP\n",
>         "M=M+1\n",
>         NULL
>     );
> }
> 
> // pop R{registerNumber}
> void writePopRegister(FILE* fpAsm, int registerNumber)
> {
>     char symbol[8];
>     sprintf(symbol, "R%d", registerNumber);
> 
>     fputslist(
>         fpAsm,
>         // Memory[SP] -= 1
>         "@SP\n",
>         "M=M-1\n",
>         // register <- Memory[Memory[SP]]
>         "@SP\n",
>         "A=M\n",
>         "D=M\n",
>         "@", symbol, "\n",
>         "M=D\n",
>         NULL
>     );
> }
>

8章（プログラム制御）

プログラムフローコマンド

ソースコードは08/VMtranslator3/です。

ここでは下記のコマンドに対応しました。

コマンド	概要
label xxx	(vmFileName$xxx)
goto xxx	jump to vmFileName$xxx
if-goto xxx	pop y, if y != 0(false/0x0000) then jump to vmFileName$xxx

下記で使えます。

test08.sh:L8-L31

cp ./nand2tetris/projects/08/ProgramFlow/BasicLoop/* 08/VMtranslator3/

# ...(省略)...

cd 08/VMtranslator3/

clang --std=c11 -Wall -Wextra -o VMtranslator main.c Parser.c ParserPrivate.c CodeWriter.c CodeWriterPrivate.c

# ...(省略)...
./VMtranslator BasicLoop.vm

main.c

label, goto, if-gotoに対応しました。

$ diff -w -r 07/VMtranslator2/main.c 08/VMtranslator3/main.c 
235a236,247
>         case PARSER_COMMAND_TYPE_C_LABEL:
>             Parser_arg1(parser, segment);
>             CodeWriter_writeLabel(codeWriter, segment);
>             break;
>         case PARSER_COMMAND_TYPE_C_GOTO:
>             Parser_arg1(parser, segment);
>             CodeWriter_writeGoto(codeWriter, segment);
>             break;
>         case PARSER_COMMAND_TYPE_C_IF:
>             Parser_arg1(parser, segment);
>             CodeWriter_writeIf(codeWriter, segment);
>             break;

Parserモジュール

label, goto, if-gotoに対応しました。

$ diff -w -r 07/VMtranslator2/Parser.h 08/VMtranslator3/Parser.h
7c7
< #define PARSER_COMMAND_MAX_LENGTH (4)
---
> #define PARSER_COMMAND_MAX_LENGTH (8)
14c14,17
<     PARSER_COMMAND_TYPE_C_POP
---
>     PARSER_COMMAND_TYPE_C_POP,
>     PARSER_COMMAND_TYPE_C_LABEL,
>     PARSER_COMMAND_TYPE_C_GOTO,
>     PARSER_COMMAND_TYPE_C_IF
$ diff -w -r 07/VMtranslator2/Parser.c 08/VMtranslator3/Parser.c
46a47,53
>     case PARSER_COMMAND_TYPE_C_LABEL:
>     case PARSER_COMMAND_TYPE_C_GOTO:
>     case PARSER_COMMAND_TYPE_C_IF:
>         skipSpaces(thisObject->fpVm);
>         getToken(thisObject->fpVm, thisObject->arg1);
>         strcpy(thisObject->arg2, "");
>         break;
68a76,78
>     IF_CMP_RET(thisObject->command,   "label", PARSER_COMMAND_TYPE_C_LABEL);
>     IF_CMP_RET(thisObject->command,    "goto", PARSER_COMMAND_TYPE_C_GOTO);
>     IF_CMP_RET(thisObject->command, "if-goto", PARSER_COMMAND_TYPE_C_IF);
$ diff -w -r 07/VMtranslator2/ParserPrivate.h 08/VMtranslator3/ParserPrivate.h
$ diff -w -r 07/VMtranslator2/ParserPrivate.c 08/VMtranslator3/ParserPrivate.c

CodeWriterモジュール

label, goto, if-gotoに対応しました。

$ diff -w -r 07/VMtranslator2/CodeWriter.h 08/VMtranslator3/CodeWriter.h
19a20,22
> void CodeWriter_writeLabel(CodeWriter thisObject, char *label);
> void CodeWriter_writeGoto(CodeWriter thisObject, char *label);
> void CodeWriter_writeIf(CodeWriter thisObject, char *label);
$ diff -w -r 07/VMtranslator2/CodeWriter.c 08/VMtranslator3/CodeWriter.c
5a6
> #define LABEL_SYMBOL_MAX_LENGTH (CODE_WRITER_VM_FILENAME_MAX_LENGTH + 24)
81a83,129
> void CodeWriter_writeLabel(CodeWriter thisObject, char *label)
> {
>     char labelSymbol[LABEL_SYMBOL_MAX_LENGTH + 1];
>     sprintf(labelSymbol, "%s$%s", thisObject->vmFileName, label);
> 
>     fputslist(
>         thisObject->fpAsm,
>         "(", labelSymbol, ")\n",
>         NULL
>     );
> }
> 
> void CodeWriter_writeGoto(CodeWriter thisObject, char *label)
> {
>     char labelSymbol[LABEL_SYMBOL_MAX_LENGTH + 1];
>     sprintf(labelSymbol, "%s$%s", thisObject->vmFileName, label);
> 
>     fputslist(
>         thisObject->fpAsm,
>         // goto labelSymbol
>         "@", labelSymbol, "\n",
>         "0;JMP\n",
>         NULL
>     );
> }
> 
> void CodeWriter_writeIf(CodeWriter thisObject, char *label)
> {
>     char labelSymbol[LABEL_SYMBOL_MAX_LENGTH + 1];
>     sprintf(labelSymbol, "%s$%s", thisObject->vmFileName, label);
> 
>     fputslist(
>         thisObject->fpAsm,
>         // Memory[SP] -= 1
>         "@SP\n",
>         "M=M-1\n",
>         // Register <- Memory[Memory[SP]]
>         "@SP\n",
>         "A=M\n",
>         "D=M\n",
>         // if jump(Register != 0) then goto labelSymbol
>         "@", labelSymbol, "\n",
>         "D;JNE\n",
>         NULL
>     );
> }
> 
$ diff -w -r 07/VMtranslator2/CodeWriterPrivate.h 08/VMtranslator3/CodeWriterPrivate.h
$ diff -w -r 07/VMtranslator2/CodeWriterPrivate.c 08/VMtranslator3/CodeWriterPrivate.c

関数呼び出しコマンド（ブートストラップなし）

ソースコードは08/VMtranslator4/です。

ここでは下記のコマンドに対応しました。

コマンド	概要
function f n	(f), push 0 repeat n
return	各種レジスタ復元, goto リターンアドレス

下記で使えます。

test08.sh:L40-L64

cp ./nand2tetris/projects/08/FunctionCalls/SimpleFunction/* 08/VMtranslator4/

# ...(省略)...

cd 08/VMtranslator4/

clang --std=c11 -Wall -Wextra -o VMtranslator main.c Parser.c ParserPrivate.c CodeWriter.c CodeWriterPrivate.c

# ...(省略)...
./VMtranslator SimpleFunction.vm

main.c

function, returnに対応しました。

$ diff -w -r 08/VMtranslator3/main.c 08/VMtranslator4/main.c 
247a248,254
>         case PARSER_COMMAND_TYPE_C_RETURN:
>             CodeWriter_writeReturn(codeWriter);
>             break;
>         case PARSER_COMMAND_TYPE_C_FUNCTION:
>             Parser_arg1(parser, segment);
>             CodeWriter_writeFunction(codeWriter, segment, Parser_arg2(parser));
>             break;

Parserモジュール

function, returnに対応しました。

$ diff -w -r 08/VMtranslator3/Parser.h 08/VMtranslator4/Parser.h
7,8c7,8
< #define PARSER_COMMAND_MAX_LENGTH (8)
< #define PARSER_ARG1_MAX_LENGTH    (8)
---
> #define PARSER_COMMAND_MAX_LENGTH (16)
> #define PARSER_ARG1_MAX_LENGTH    (32)
17c17,19
<     PARSER_COMMAND_TYPE_C_IF
---
>     PARSER_COMMAND_TYPE_C_IF,
>     PARSER_COMMAND_TYPE_C_FUNCTION,
>     PARSER_COMMAND_TYPE_C_RETURN
$ diff -w -r 08/VMtranslator3/Parser.c 08/VMtranslator4/Parser.c
41a42
>     case PARSER_COMMAND_TYPE_C_FUNCTION:
53a55
>     case PARSER_COMMAND_TYPE_C_RETURN:
78a81,82
>     IF_CMP_RET(thisObject->command, "function", PARSER_COMMAND_TYPE_C_FUNCTION);
>     IF_CMP_RET(thisObject->command,   "return", PARSER_COMMAND_TYPE_C_RETURN);
95c99,100
<         Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_POP) {
---
>         Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_POP ||
>         Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_FUNCTION) {
$ diff -w -r 08/VMtranslator3/ParserPrivate.h 08/VMtranslator4/ParserPrivate.h 
$ diff -w -r 08/VMtranslator3/ParserPrivate.c 08/VMtranslator4/ParserPrivate.c

CodeWriterモジュール

function, returnに対応しました。

$ diff -w -r 08/VMtranslator3/CodeWriter.h 08/VMtranslator4/CodeWriter.h 
22a23,24
> void CodeWriter_writeReturn(CodeWriter thisObject);
> void CodeWriter_writeFunction(CodeWriter thisObject, char *functionName, int numLocals);
$ diff -w -r 08/VMtranslator3/CodeWriter.c 08/VMtranslator4/CodeWriter.c
129a130,218
> void CodeWriter_writeReturn(CodeWriter thisObject)
> {
>     fputslist(
>         thisObject->fpAsm,
>         "// return\n",
>         // Memory[R13] <- Memory[LCL]
>         "@LCL\n",
>         "D=M\n",
>         "@R13\n",
>         "M=D\n",
>         // Memory[R14] <- Memory[Memory[R13]-5]
>         "@5\n",
>         "D=A\n",
>         "@R13\n",
>         "A=M-D\n",
>         "D=M\n",
>         "@R14\n",
>         "M=D\n",
>         // Memory[SP] -= 1
>         "@SP\n",
>         "M=M-1\n",
>         // Memory[Memory[ARG]] <- Memory[Memory[SP]]
>         "@SP\n",
>         "A=M\n",
>         "D=M\n",
>         "@ARG\n",
>         "A=M\n",
>         "M=D\n",
>         // Memory[SP] <- Memory[ARG] + 1
>         "@ARG\n",
>         "D=M+1\n",
>         "@SP\n",
>         "M=D\n",
>         // Memory[THAT] <- Memory[Memory[R13]-1]
>         "@1\n",
>         "D=A\n",
>         "@R13\n",
>         "A=M-D\n",
>         "D=M\n",
>         "@THAT\n",
>         "M=D\n",
>         // Memory[THIS] <- Memory[Memory[R13]-2]
>         "@2\n",
>         "D=A\n",
>         "@R13\n",
>         "A=M-D\n",
>         "D=M\n",
>         "@THIS\n",
>         "M=D\n",
>         // Memory[ARG] <- Memory[Memory[R13]-3]
>         "@3\n",
>         "D=A\n",
>         "@R13\n",
>         "A=M-D\n",
>         "D=M\n",
>         "@ARG\n",
>         "M=D\n",
>         // Memory[LCL] <- Memory[Memory[R13]-4]
>         "@4\n",
>         "D=A\n",
>         "@R13\n",
>         "A=M-D\n",
>         "D=M\n",
>         "@LCL\n",
>         "M=D\n",
>         // goto Memory[R14]
>         "@R14\n",
>         "A=M\n",
>         "0;JMP\n",
>         NULL
>     );
> }
> 
> void CodeWriter_writeFunction(CodeWriter thisObject, char *functionName, int numLocals)
> {
>     char numLocalsString[255];
>     sprintf(numLocalsString, "%d", numLocals);
> 
>     fputslist(
>         thisObject->fpAsm,
>         "// function ", functionName, " ", numLocalsString, "\n",
>         "(", functionName, ")\n",
>         NULL
>     );
>     for (int i = 0; i < numLocals; i++) {
>         writePushConstant(thisObject->fpAsm, 0);
>     }
> }
> 
$ diff -w -r 08/VMtranslator3/CodeWriterPrivate.h 08/VMtranslator4/CodeWriterPrivate.h
$ diff -w -r 08/VMtranslator3/CodeWriterPrivate.c 08/VMtranslator4/CodeWriterPrivate.c

関数呼び出しコマンド（完全版）

ソースコードは08/VMtranslator5/です。

ここでは下記のコマンドに対応しました。また、ブートストラップコードに対応したので.vmファイルには必ずSys.init関数が必要です。

コマンド	概要
call f m	各種レジスタ保存, goto f

下記で使えます。

test08.sh:L66-L82

cp -r ./nand2tetris/projects/08/FunctionCalls/FibonacciElement 08/VMtranslator5/

# ...(省略)...

cd 08/VMtranslator5/

clang --std=c11 -Wall -Wextra -o VMtranslator main.c Parser.c ParserPrivate.c CodeWriter.c CodeWriterPrivate.c

# ...(省略)...
./VMtranslator FibonacciElement

main.c

callおよび複数vmファイルに対応しました。

$ diff -w -r 08/VMtranslator4/main.c 08/VMtranslator5/main.c 
80a81
>     CodeWriter_writeInit(codeWriter);
114,115d114
< 
<         break;
163c162
< 
---
>     CodeWriter_writeInit(codeWriter);
247a247,250
>         case PARSER_COMMAND_TYPE_C_CALL:
>             Parser_arg1(parser, segment);
>             CodeWriter_writeCall(codeWriter, segment, Parser_arg2(parser));
>             break;

Parserモジュール

callに対応しました。

$ diff -w -r 08/VMtranslator4/Parser.h 08/VMtranslator5/Parser.h 
19c19,20
<     PARSER_COMMAND_TYPE_C_RETURN
---
>     PARSER_COMMAND_TYPE_C_RETURN,
>     PARSER_COMMAND_TYPE_C_CALL
$ diff -w -r 08/VMtranslator4/Parser.c 08/VMtranslator5/Parser.c
42a43
>     case PARSER_COMMAND_TYPE_C_CALL:
82a84
>     IF_CMP_RET(thisObject->command,     "call", PARSER_COMMAND_TYPE_C_CALL);
100c102,103
<         Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_FUNCTION) {
---
>         Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_FUNCTION ||
>         Parser_commandType(thisObject) == PARSER_COMMAND_TYPE_C_CALL) {
$ diff -w -r 08/VMtranslator4/ParserPrivate.h 08/VMtranslator5/ParserPrivate.h
$ diff -w -r 08/VMtranslator4/ParserPrivate.c 08/VMtranslator5/ParserPrivate.c

CodeWriterモジュール

callおよび複数vmファイルに対応しました。

$ diff -w -r 08/VMtranslator4/CodeWriter.h 08/VMtranslator5/CodeWriter.h 
12a13
> void CodeWriter_writeInit(CodeWriter thisObject);
22a24
> void CodeWriter_writeCall(CodeWriter thisObject, char *functionName, int numArgs);
$ diff -w -r 08/VMtranslator4/CodeWriter.c 08/VMtranslator5/CodeWriter.c
10a11
> void writePushRegisterByName(FILE* fpAsm, char *registerName);
18a20
>     int callCount;
26a29
>     thisObject.callCount = 0;
38a42,56
> void CodeWriter_writeInit(CodeWriter thisObject)
> {
>     fputslist(
>         thisObject->fpAsm,
>         // Memory[SP] <- 256
>         "@256\n",
>         "D=A\n",
>         "@SP\n",
>         "M=D\n",
>         NULL
>     );
>     // call Sys.init 0
>     CodeWriter_writeCall(thisObject, "Sys.init", 0);
> }
> 
129a148,203
> void CodeWriter_writeCall(CodeWriter thisObject, char *functionName, int numArgs)
> {
>     char numArgsString[255];
>     sprintf(numArgsString, "%d", numArgs);
> 
>     char returnLabel[255];
>     sprintf(returnLabel, "%s$%d", functionName, thisObject->callCount);
> 
>     fputslist(
>         thisObject->fpAsm,
>         "// call ", functionName, " ", numArgsString, "\n",
>         // Memory[Memory[SP]] <- return-address
>         "@", returnLabel, "\n",
>         "D=A\n",
>         "@SP\n",
>         "A=M\n",
>         "M=D\n",
>         // Memory[SP] += 1
>         "@SP\n",
>         "M=M+1\n",
>         NULL
>     );
> 
>     // push LCL, ARG, THIS, THAT
>     writePushRegisterByName(thisObject->fpAsm, "LCL");
>     writePushRegisterByName(thisObject->fpAsm, "ARG");
>     writePushRegisterByName(thisObject->fpAsm, "THIS");
>     writePushRegisterByName(thisObject->fpAsm, "THAT");
> 
>     fputslist(
>         thisObject->fpAsm,
>         // Memory[ARG] <- Memory[SP]-numArgsString-5
>         "@SP\n",
>         "D=M\n",
>         "@", numArgsString, "\n",
>         "D=D-A\n",
>         "@5\n",
>         "D=D-A\n",
>         "@ARG\n",
>         "M=D\n",
>         // Memory[LCL] <- Memory[SP]
>         "@SP\n",
>         "D=M\n",
>         "@LCL\n",
>         "M=D\n",
>         // goto function
>         "@", functionName, "\n",
>         "0;JMP\n",
>         // (return-address) <- {thisObject->vmFileName}${thisObject->callCount}
>         "(", returnLabel, ")\n",
>         NULL
>     );
> 
>     thisObject->callCount++;
> }
> 
246a321,337
> 
> void writePushRegisterByName(FILE* fpAsm, char *registerName)
> {
>     fputslist(
>         fpAsm,
>         // Memory[Memory[SP]] <- Memory[registerName]
>         "@", registerName, "\n",
>         "D=M\n",
>         "@SP\n",
>         "A=M\n",
>         "M=D\n",
>         // Memory[SP] += 1
>         "@SP\n",
>         "M=M+1\n",
>         NULL
>     );
> }
$ diff -w -r 08/VMtranslator4/CodeWriterPrivate.h 08/VMtranslator5/CodeWriterPrivate.h
$ diff -w -r 08/VMtranslator4/CodeWriterPrivate.c 08/VMtranslator5/CodeWriterPrivate.c

まとめ

なんとなくは知っていたはずのバーチャルマシンも実際に実装してみようと思うと大変でした。特にコマンドに対応するアセンブラを考えるのは頭の体操になりました。また相変わらずC言語はディレクトリ、ファイル、文字列操作など大変と感じました。色々怪しい実装部分は残っていますがとりあえず動かせたのはよかったです。

a == 0	a == 1	c	c	c	c	c	c
0	-	1	0	1	0	1	0
1	-	1	1	1	1	1	1
-1	-	1	1	1	0	1	0
D	-	0	0	1	1	0	0
A	M	1	1	0	0	0	0
!D	-	0	0	1	1	0	1
!A	!M	1	1	0	0	0	1
-D	-	0	0	1	1	1	1
-A	-M	1	1	0	0	1	1
D+1	-	0	1	1	1	1	1
A+1	M+1	1	1	0	1	1	1
D-1	-	0	0	1	1	1	0
A-1	M-1	1	1	0	0	1	0
D+A	D+M	0	0	0	0	1	0
D-A	D-M	0	1	0	0	1	1
A-D	M-D	0	0	0	1	1	1
D&A	D&M	0	0	0	0	0	0
D\|A	D\|M	0	1	0	1	0	1

a == 0	a == 1	c	c	c	c	c	c
0	-	1	0	1	0	1	0
1	-	1	1	1	1	1	1
-1	-	1	1	1	0	1	0
D	-	0	0	1	1	0	0
A	M	1	1	0	0	0	0
!D	-	0	0	1	1	0	1
!A	!M	1	1	0	0	0	1
-D	-	0	0	1	1	1	1
-A	-M	1	1	0	0	1	1
D+1	-	0	1	1	1	1	1
A+1	M+1	1	1	0	1	1	1
D-1	-	0	0	1	1	1	0
A-1	M-1	1	1	0	0	1	0
D+A	D+M	0	0	0	0	1	0
D-A	D-M	0	1	0	0	1	1
A-D	M-D	0	0	0	1	1	1
D&A	D&M	0	0	0	0	0	0
D\|A	D\|M	0	1	0	1	0	1

a == 0	a == 1	c	c	c	c	c	c
0	-	1	0	1	0	1	0
1	-	1	1	1	1	1	1
-1	-	1	1	1	0	1	0
D	-	0	0	1	1	0	0
A	M	1	1	0	0	0	0
!D	-	0	0	1	1	0	1
!A	!M	1	1	0	0	0	1
-D	-	0	0	1	1	1	1
-A	-M	1	1	0	0	1	1
D+1	-	0	1	1	1	1	1
A+1	M+1	1	1	0	1	1	1
D-1	-	0	0	1	1	1	0
A-1	M-1	1	1	0	0	1	0
D+A	D+M	0	0	0	0	1	0
D-A	D-M	0	1	0	0	1	1
A-D	M-D	0	0	0	1	1	1
D&A	D&M	0	0	0	0	0	0
D\|A	D\|M	0	1	0	1	0	1