関数プログラミング 珠玉のアルゴリズムデザインの第19章の"単純な数独ソルバー"のアルゴリズムを追いました。 各効率化の戦略を読み解くのが大変だったので後でまた読むときのために概要だけメモを残します。
お題は数独ソルバー
数独を解くアルゴリズムをプログラム運算により効率の良いものにしていきます。言語はHaskellです。
数独は次のようなゲームです。
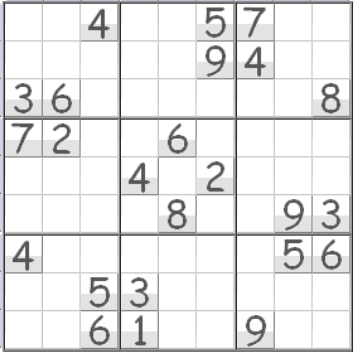
ルール
・空いているマスに1〜9のいずれかの数字を入れる。
・縦・横の各列及び、太線で囲まれた3×3のブロック内に同じ数字が複数入ってはいけない。
最初のアルゴリズム
最初のアルゴリズムは次のような愚直な感じの流れです。
(答えの候補が膨大なので処理が終わらないです。)
- 空のマス目に入る候補を1〜9とする。
- すべての空のマス目の候補の組み合わせで答えの候補を作る。
- 答えの候補から数独ルールに合っているものを取り出して答えとする。
Haskellプログラムの実行イメージは次のような感じです。
solve = filter valid . expand . choices {- 問題データ:空のマス目は0 ["004005700", "000009400", "360000008", "720060000", "000402000", "000080093", "400000056", "005300000", "006100900"] ↓ choices:空のマス目を候補の数値にする [["123456789","123456789","4","123456789","123456789","5","7","123456789","123456789"], ["123456789","123456789","123456789","123456789","123456789","9","4","123456789","123456789"], ["3","6","123456789","123456789","123456789","123456789","123456789","123456789","8"], ["7","2","123456789","123456789","6","123456789","123456789","123456789","123456789"], ["123456789","123456789","123456789","4","123456789","2","123456789","123456789","123456789"], ["123456789","123456789","123456789","123456789","8","123456789","123456789","9","3"], ["4","123456789","123456789","123456789","123456789","123456789","123456789","5","6"], ["123456789","123456789","5","3","123456789","123456789","123456789","123456789","123456789"], ["123456789","123456789","6","1","123456789","123456789","9","123456789","123456789"]] ↓ expand:空のマス目の候補すべて組み合わせで答えの候補を作る [[["114115711"], <- 1xxx ["111119411"], ["361111118"], ["721161111"], ["111412111"], ["111181193"], ["411111156"], ["115311111"], ["116111911"]], [["214115711"], <- 2xxx ["111119411"], ["361111118"], ["721161111"], ["111412111"], ["111181193"], ["411111156"], ["115311111"], ["116111911"]], [["314115711"], <- 3xxx ["111119411"], ["361111118"], ["721161111"], ["111412111"], ["111181193"], ["411111156"], ["115311111"], ["116111911"]], ・・・, [["994995799"], ["999999499"], ["369999998"], ["729969999"], ["999492999"], ["999989993"], ["499999956"], ["995399999"], ["996199999"]]] ↓ (filter valid):数独ルールに合っている答えの候補のみ取り出す 答え:1つとは限らない [["184625739", "572839461", "369741528", "728963145", "953412687", "641587293", "417298356", "295376814", "836154972"]] -}
選択肢行列の枝刈り
最初のアルゴリズムで空のマス目に入る候補を1〜9としていたところから、数独ルールに合わない候補を無くします。
例えば空のマス目の数が30、そこに入る候補の数の平均が4になるとすれば探索範囲数は下記のようにしぼられます。(これでも処理時間は相当かかります。)
42391158275216203514294433201(9の30乗)→1152921504606846976(4の30乗)
Haskellプログラムの実行イメージは次のような感じです。
solve = filter valid . expand . prune . choices {- 問題データ:空のマス目は0 ↓ choices:空のマス目を候補の数値にする ↓ prune:無効な空のマス目候補を排除する [["1289","189","4","268","123","5","7","1236","129"], ["1258","1578","1278","2678","1237","9","4","1236","125"], ["3","6","1279","27","1247","147","125","12","8"], ["7","2","1389","59","6","13","158","148","145"], ["15689","13589","1389","4","13579","2","1568","1678","157"], ["156","145","1","57","8","17","1256","9","3"], ["4","13789","123789","2789","279","78","1238","5","6"], ["1289","1789","5","3","2479","4678","128","12478","1247"], ["28","378","6","1","2457","478","9","23478","247"]] ↓ expand:空のマス目候補すべて組み合わせで答えの候補を作る ↓ (filter valid):数独ルールに合っている答えの候補のみ取り出す 答え:1つとは限らない -}
単一マス拡張
空のマス目1マスずつ逐次的に"答えの候補の作成"と"無効な空のマス目候補の排除"を行う事で探索範囲数の大幅な削減を期待します。 (相当速くなります。)
Haskellプログラムの実行イメージは次のような感じです。
solve = search . choices search m | not $ safe m = [] | complete m' = [map (map head) m'] | otherwise = concat (map search (expand1 m')) where m' = prune m {- 問題データ:空のマス目は0 ↓ choices:空のマス目を候補の数値にする ↓ search:答えを探索する(再帰する) ↑↓ prune:無効な空のマス目候補を排除する ↑↓ expand1:空のマス目候補の少ないマス目を1つだけ選び答えの候補を作る [[["1289","189","4","268","123","5","7","1236","129"], ["1258","1578","1278","2678","1237","9","4","1236","125"], ["3","6","1279", "2", <- "1247","147","125","12","8"], ["7","2","1389","59","6","13","158","148","145"], ["15689","13589","1389","4","13579","2","1568","1678","157"], ["156","145","1","57","8","17","1256","9","3"], ["4","13789","123789","2789","279","78","1238","5","6"], ["1289","1789","5","3","2479","4678","128","12478","1247"], ["28","378","6","1","2457","478","9","23478","247"]], [["1289","189","4","268","123","5","7","1236","129"], ["1258","1578","1278","2678","1237","9","4","1236","125"], ["3","6","1279", "7", <- "1247","147","125","12","8"], ["7","2","1389","59","6","13","158","148","145"], ["15689","13589","1389","4","13579","2","1568","1678","157"], ["156","145","1","57","8","17","1256","9","3"], ["4","13789","123789","2789","279","78","1238","5","6"], ["1289","1789","5","3","2479","4678","128","12478","1247"], ["28","378","6","1","2457","478","9","23478","247"]]] ↓ すべてが not $ safe または complete になったら再帰終了 答え:1つとは限らない -}
感想等
- 関数プログラミング 珠玉のアルゴリズムデザイン面白いです。図があまり無いのでイメージが湧かない面もあり手を動かす必要があると思いますが(時間があれば...)手を動かすのも楽しいです。関数プログラミング実践入門の第6章でも数独の実装例があるので読み比べるのも勉強になります。
- 動かすとき下記は自分で定義しました。
import Data.List ((\\)) -- 単一要素リストであることを検査する関数 single :: [a] -> Bool single [_] = True single _ = False